Вариант 07 Выполните действия в тригонометрической форме. Результат запишите в показательной и
алгебраической формах: 4(cos 220°+i sin 220°
) * (cos 20° +i sin 20°
).
Проверьте, является ли верным высказывание: в треугольнике с вершинами А(-1,-3),В(4,-5),
С(2, 1) высота BD имеет уравнение Зх+4у+8=0. Сделайте чертеж.
Найдите производную функции y=tg2
x-ctg2
x и вычислите у'(п/4).
Найдите интегралы:
6)
J(з sin х + 4 х
3
- 1 }ix f
2
-
1/x
dx х1/х
5.
а)
Вычислите определенные интегралы:
,r
f 2sinxdx
о
б)
6. Сделайте чертеж и вычислите площадь фигуры, ограниченной данными линиями:
у=х
2
-4х-5 и осью Ох
Замена: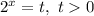
Имеем квадратичную функцию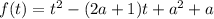 , графиком которой является парабола с ветвями, направленными вверх.
, графиком которой является парабола с ветвями, направленными вверх.
Найдем возможные точки пересечения параболы с осью абсцисс.
Для этого решим квадратное уравнение:
Найдем дискриминант данного уравнения:
Имеем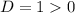 , значит данное уравнение имеет ровно 2 корня:
, значит данное уравнение имеет ровно 2 корня:
Имеем две точки пересечения параболы с осью абсцисс.
Пусть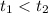 . Тогда
. Тогда 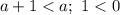 . Имеем неверное неравенство. Следовательно, при всех значениях параметра
. Имеем неверное неравенство. Следовательно, при всех значениях параметра  имеем
имеем 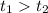 .
.
Тогда квадратичная функция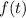 будет меньше 0 при
будет меньше 0 при 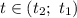
Последнее можно записать так:
Обратная замена:
Если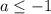 , то имеем:
, то имеем: 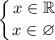
Решением такой системы неравенств является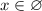
Если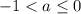 , то имеем:
, то имеем: 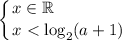
Решением такой системы неравенств является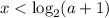
Если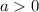 , то имеем:
, то имеем: 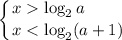
Решением такой системы неравенств является интервал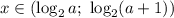
еслиПроверим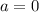 : имеем уравнение
: имеем уравнение 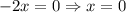 - очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
- очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.
При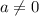 уравнение - квадратное вида
уравнение - квадратное вида 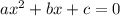 . Коэффициенты:
. Коэффициенты:  (внезапно),
(внезапно), 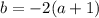 ,
,  . Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
. Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.
Ищем дискриминант:
Найдем дискриминант трехчлена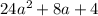 :
: 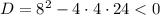
Это значит что при любых выражение
выражение 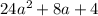
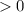 , т.е. исходное уравнение всегда имеет 2 корня.
, т.е. исходное уравнение всегда имеет 2 корня.
Могут быть три ситуации: 1) оба корня отрицательные; 2) корни имеют разные знаки; 3) оба корня положительные. Условию (нужно как минимум одно положительное решение) удовлетворяют только 2 и 3.
Проверим второй случай. Если корни имеют разные знаки, то достаточно условия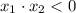 . По теореме Виета
. По теореме Виета 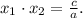 Так как в нашем случае
Так как в нашем случае 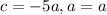 , то
, то 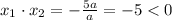 при любых
при любых  . Т.е. при любых значениях параметра (кроме
. Т.е. при любых значениях параметра (кроме 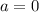 ) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.
Значит, нас устраивают любые , кроме
, кроме 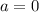 .
.
ОТВЕТ: при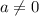 .
.