1. q = -2.
2. 1;1/2;1/4 q = 1/2
1;3;9q = 3
2/3;1/2;3/8q = 3/4
√2; 1;√2/2q = 1/√2
3. заданная формула возможно неточно переписана или последовательность не геометрическая.
3*2n - 3 умножить на 2n или 3 возвести в степень 2n
4. q = 0,5
5. S = -0.25
6. b6 = 243.
7. 3-n,3-2n,3-3n,3-4n, 3n,3n+1,3n+2,3n+3 - єти последовательности не являются геометрическими прогрессиями
Объяснение:
1. Последовательность геометрическая т.к. а2 = а1 * q, а3 = а2 * q, где
q - одно и тоже число (знаменатель данной геометрической прогрессии)
q = а2 / а1 = -6 / 3 = -2.
4. Из формулы нахождения n-го члена геометрической прогрессии
q = а2 / а1 = 10/20 = 0,5.
5. q = а2 / а1 = -2/4 = -0,5
а5 = 4 * (-0,5)^4 = 0.25
a4 = 4 * (-0.5) ^3 = -0.5
6. b6 = b1 * q^5 = 243.
В базисе векторы имеют следующие координаты:
Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.
Докажем компланарность векторов двумя
школьный (≈10 класс)
Признак компланарности трёх векторов:
Пусть векторы и не коллинеарны. Если для вектора существует единственная пара реальных чисел A и B, такая, что , то векторы компланарны.
Покажем, что
Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:
Сложим первое и второе уравнение, получим:
-1 = B
Подставим значение B в первое уравнение, найдём A:
3 = -A - (-1)
A = -2
Проверим найденные значения для остальных уравнений системы.
Итого получаем:
То есть признак выполнен. Значит векторы компланарны.
обычно проходится в вузах):
Векторы компланарны, если
Проверим это условие для данных векторов:
Следовательно, векторы компланарны.
1. q = -2.
2. 1;1/2;1/4 q = 1/2
1;3;9q = 3
2/3;1/2;3/8q = 3/4
√2; 1;√2/2q = 1/√2
3. заданная формула возможно неточно переписана или последовательность не геометрическая.
3*2n - 3 умножить на 2n или 3 возвести в степень 2n
4. q = 0,5
5. S = -0.25
6. b6 = 243.
7. 3-n,3-2n,3-3n,3-4n, 3n,3n+1,3n+2,3n+3 - єти последовательности не являются геометрическими прогрессиями
Объяснение:
1. Последовательность геометрическая т.к. а2 = а1 * q, а3 = а2 * q, где
q - одно и тоже число (знаменатель данной геометрической прогрессии)
q = а2 / а1 = -6 / 3 = -2.
4. Из формулы нахождения n-го члена геометрической прогрессии
q = а2 / а1 = 10/20 = 0,5.
5. q = а2 / а1 = -2/4 = -0,5
а5 = 4 * (-0,5)^4 = 0.25
a4 = 4 * (-0.5) ^3 = -0.5
6. b6 = b1 * q^5 = 243.
В базисе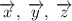 векторы имеют следующие координаты:
векторы имеют следующие координаты:
Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.
Докажем компланарность векторов двумя
школьный (≈10 класс)
Признак компланарности трёх векторов:
Пусть векторы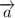 и
и 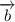 не коллинеарны. Если для вектора
не коллинеарны. Если для вектора 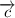 существует единственная пара реальных чисел A и B, такая, что
существует единственная пара реальных чисел A и B, такая, что  , то векторы
, то векторы 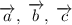 компланарны.
компланарны.
Покажем, что
Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:
Сложим первое и второе уравнение, получим:
-1 = B
Подставим значение B в первое уравнение, найдём A:
3 = -A - (-1)
A = -2
Проверим найденные значения для остальных уравнений системы.
Итого получаем:
То есть признак выполнен. Значит векторы компланарны.
обычно проходится в вузах):
Векторы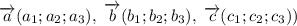 компланарны, если
компланарны, если
Проверим это условие для данных векторов:
Следовательно, векторы компланарны.