для начала находим корни данного в условии уравнения x^2-3x+1=0
D=9-4=13
x1=[3+кореньиз(13)]/2
x2=[3-кореньиз(13)]/2
Составьте уравнение корни которого на 1 больше корней уравнени:
Наши новые корни X=x1+1 и X=x2+1 получаем X=[5+кореньиз(13)]/2
X=[5-кореньиз(13)]/2
Воспользуемся теоремой Виета ,которая говорит нам: x^2+px+q=0
x1+x2=-p
x1*x2=q
Подставим в эту теорему наши новые корни (которые на 1 больше старых ):
[5+кореньиз(13)]/2+[5-кореньиз(13)]/2=-p
[5+кореньиз(13)]/2*[5-кореньиз(13)]/2=q
Таким образом наше квадратное уравнение (которое просят составить в условии) примет вид : x^2-5x+[(25-13)]/2=0-->> конечный вид x^2-5x+6=0
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если , а , при k>5
То есть, , при k>5, то по закону транзитивности:
, при k>5 - ч.т.д
для начала находим корни данного в условии уравнения x^2-3x+1=0
D=9-4=13
x1=[3+кореньиз(13)]/2
x2=[3-кореньиз(13)]/2
Составьте уравнение корни которого на 1 больше корней уравнени:
Наши новые корни X=x1+1 и X=x2+1 получаем X=[5+кореньиз(13)]/2
X=[5-кореньиз(13)]/2
Воспользуемся теоремой Виета ,которая говорит нам: x^2+px+q=0
x1+x2=-p
x1*x2=q
Подставим в эту теорему наши новые корни (которые на 1 больше старых ):
[5+кореньиз(13)]/2+[5-кореньиз(13)]/2=-p
[5+кореньиз(13)]/2*[5-кореньиз(13)]/2=q
Таким образом наше квадратное уравнение (которое просят составить в условии) примет вид : x^2-5x+[(25-13)]/2=0-->> конечный вид x^2-5x+6=0
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если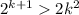 , а
, а 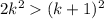 , при k>5
, при k>5
То есть,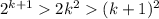 , при k>5, то по закону транзитивности:
, при k>5, то по закону транзитивности: