Под действием силы 50 H тело движется по прямой так, что его координата меняется по закону: x=10-20 t+t^2 (м). Найдите массу тела.

1) тонка лінза - це лінза в якої товщина мала порівняно з радіусами сферичних поверхонь, що її обмежують. 
2) головний фокус - це точки, в якій збігаються промені колімованого пучка світла, що перед оптичною системою проходив паралельно оптичній осі.
3) формула тонкої лінзи 
 
4)При побудові зображень створених двоопуклою лінзою, проводять три лінії:
1 - Із вершини предмета паралельно оптичній осі лінзи до головної площини лінзи, далі, заломлюючись, через задній головний фокус.
2 -І з вершини предмета через центр лінзи.
3 - Із вершини предмета через передній фокус до головної площини лінзи, а далі паралельно оптичній осі лінзи.
5) лінійне збільшення лінзи - це відношення лінійного розміру зображення до лінійного розміру предмета

1) ∠ВАС = 2∠BAD = 2 · 69° = 138°, так как AD биссектриса угла ВАС.

Сумма углов треугольника равна 180°. Из ΔАВС:

∠АВС = 180° - (∠ВАС + ∠АСВ) = 180° - (138° + 30°) = 12°

Из ΔADB:

∠ADB = 180° - (∠BAD + ∠ABD) = 180° - (69° + 12°) = 99°

2) Сумма острых углов прямоугольного треугольника равна 90°.

Пусть ∠1 = х, тогда ∠2 =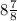 х.

∠1 + ∠2 = 90°

∠2 =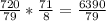

Если же в условии в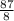 раза больше, то

∠2 =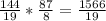

3) Углы при основании равнобедренного треугольника равны:

∠САВ = ∠СВА = (180° - ∠АСВ) / 2 = (180° - 78°) / 2 = 102/2 = 51°

∠CBD = 180° - ∠CBA = 180° - 51° = 129° по свойству смежных углов.

4) ∠ВАС = 2∠BAD = 2 · 39° = 78° так как AD биссектриса.

Сумма углов треугольника равна 180°. Из ΔАВС:

∠АВС = 180° - (∠ВАС + ∠АСВ) = 180° - (78° + 45°) = 180° - 123° = 57°

Из ΔABD:

∠ADB = 180° - (∠ABD + ∠BAD) = 180° - (57° + 39°) = 180° - 96° = 84°