Если сторона и два прилижащих к ней угла дного треугольника соответственно равны стороне и двум прилежащим к ней углу другого треугольника, то такие треугольники равны. Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, ∠ B = ∠ B1, AB = A1B1.
Пусть A1B2C2 – треугольник, равный треугольнику ABC. Вершина B2 расположена на луче A1B1, а вершина С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. Так как A1B2 = A1B1, то вершина B2 совпадает с вершиной B1. Так как ∠ B1A1C2 = ∠ B1A1C1 и ∠ A1B1C2 = ∠ A1B1C1, то луч A1C2 совпадает с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина С2 совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.
1. Прямая и плоскость параллельны, если не имеют общих точек.
2. Правильная призма - эта такая призма, у которой в основании правильный многоугольник и все боковые ребра перпендикулярны основанию.
3.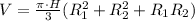
4. Плоскости параллельны, если не имеют общих точек.
5. Боковая поверхность призмы - это все параллелограмы, которые составляют боковые грани призмы. А полная - это боковая поверхность и еще основания.
6.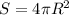
7. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
8. Параллелограм.
9. Тело, возникающее при вращении сектора вокруг одного из его радиусов.
Пусть у треугольников ABC и A1B1C1 ∠ A = ∠ A1, ∠ B = ∠ B1, AB = A1B1.
Пусть A1B2C2 – треугольник, равный треугольнику ABC. Вершина B2 расположена на луче A1B1, а вершина С2 в той же полуплоскости относительно прямой A1B1, где лежит вершина С1. Так как A1B2 = A1B1, то вершина B2 совпадает с вершиной B1. Так как ∠ B1A1C2 = ∠ B1A1C1 и ∠ A1B1C2 = ∠ A1B1C1, то луч A1C2 совпадает с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина С2 совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником A1B2C2, а значит, равен треугольнику ABC. Теорема доказана.