7.Скільки сторін у правильного многокутника, якщо його внутрішній кут дорівнює 120 градусів
А. 3
Б.4
В.5
Г.6
Д.8
Будь-ласка, напишіть розв'язок, а не тільки букву. (Дякую)
8.Чому дорівнює периметр правильного п' ятикутника, сторона якого 8√3 см?
А. 40√3 см2(в квадраті)
Б. 40√3 см
В. 64√3 см
Г. 192 см
Д. 50 см
Будь-ласка, напишіть розв'язок, а не тільки букву. (Дякую)(√ це корінь)
9.Установіть відповідність між величиною зовнішнього кута правильного многокутника та кількістю кутів многокутника
1. 120 градусів А. 3
2. 15 градусів Б. 8
3. 90 градусів В. 6
4. 45 градусів Г. 24
Д. 4
Будь-ласка, напишіть розв'язок, а не тільки букву. (Дякую)

Показать ответ

Ответ:

sergey19751975

28.03.2023 12:50

Такую задачу можно делать с теоремы о пропорциональных отрезках, но при этом нужно проводить дополнительные линии, а мне делать это лень. Поэтому воспользуемся теоремой Менелая. Советую перед разбором решения ознакомиться с формулировкой этой теоремы. А заодно и с теоремой Чевы. А если посмотрите и теорему Ван-Обеля, вы будете подкованы на 100%.

Кстати, удобно сначала воспользоваться теоремой Чевы. Поскольку чевианы PM, RK и QN пересекаются в одной точке, справедливо равенство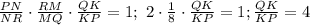 $\frac{PN}{NR}\cdot \frac{RM}{MQ}\cdot \frac{QK}{KP}=1;\ 2\cdot \frac{1}{8}\cdot \frac{QK}{KP}=1; \frac{QK}{KP}=4$ .

То есть в QK четыре части, а в KP одна часть. Следовательно, в PQ=PK+KQ пять частей, а тогда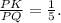 $\frac{PK}{PQ}=\frac{1}{5}.$

Для нахождения второго отношения воспользуемся теоремой Ван-Обеля. Поскольку чевианы PM, RK и QN пересекаются в точке S, то

$\frac{RS}{SK}=\frac{RN}{NP}+\frac{BM}{MQ}=\frac{1}{2}+\frac{1}{8}=\frac{5}{8}\Rightarrow \frac{KS}{SR}=\frac{8}{5}$

Для нахождения третьего отношения применим теорему Менелая к треугольнику PRS и прямой NK, которая пересекает стороны PR и PS и продолжение стороны RS. Имеем:

$\frac{PL}{LS}\cdot \frac{SK}{KR}\cdot \frac{RN}{NP}=1;$ $\frac{PL}{LS}\cdot \frac{8}{13}\cdot \frac{1}{2}=1;$

$\frac{PL}{LS}=\frac{13}{4}$

Внимание для тех, кто хочет (и знает, как) сделать сайт лучше и комфортнее! В данный момент я имею в виду не преодоление тех очевидных недостатков, которые становятся очевидными в первые пять минут, а плохую работу встроенного TEX'а. Впечатление, что здешние айтишники не знают, как решить возникающие проблемы. Предложите им свои услуги!

0,0(0 оценок)

Ответ:

Alien1712

22.05.2023 01:47

Продолжим боковые стороны до точки пересечения T. (Выходит что BC средняя линия треугольника ATD)
Проведем FO||AT ,OL||TD. Откуда подобны треугольники:
ATD и FOL,AMD и FOD,AND и AOL.
Откуда верны отношения:
FO/4y=LO/6z=FL/AD
FO/y=(FL+LD)/AD=OD/MD; FO/4y=(FL+LD)/4AD
LO/2z=(FL+AF)/AD ; LO/6z=(FL+AF)/3AD
(FL+LD)/4AD=FL/AD
FL+LD=4FL
LD=3FL
(FL+AF)/3AD=FL/AD
FL+AF=3FL
AF=2FL
OD/MD=(FL+LD)/(AF+FL+LD)=4FL/(6FL)=2/3
Проведем диагональ BD.
Треугольники ABD и BDC имеют одинаковые высоты, равные высоте трапеции. То есть их площади относятся как основы трапеции:
SBCD=SABD/2 (в сумме они дают площадь трапеции)
27cм^2=SABD+SABD/2=3SABD/2
SABD=18cм^2
Треугольники ABD и AMD имеют общую высоту,то их площади тоже относятся как их основы (AM и AB):
SAMD=SABD/2=9cм^2
Ну и наконец треугольники AMD и AOD тоже имеют общую высоты,то их площади тоже относятся как основы (OD и MD).
Из выше показанного:OD/MD=2/3
Откуда: SAOD=2SAMD/3=18/3=6cм^2
ответ:SAOD=6cм^2
Я не гарантирую ,что это самый простой путь решения.
Я даже на 100 процентов уверен,что есть попроще.

Втрапеции авсd площадью s = 27 см2 основание вс в два раза меньшеоснования аd. точка м делит боковую