Дан . найти: 1) уравнения его сторон; 2) уравнение высоты, опущенной из вершины на сторону ; 3) уравнение медианы ; 4)уравнение прямой, проходящей через точку и параллельной медиане , если a(0: -1), b(-3; 0), c(4; 2)
Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.
Тогда угол AKC 180-90-45 = 45 град.
Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.
Объяснение:
Не уверен, но вариант такой:
Т.к. АВ=3NB, то AN=2NB, следовательно AN в два раза больше NB, а значит углы напроив этих сторон отличаются в два раза и следовательно угол BKN в два раза меньше угла NKA (который 90 град), получаем, что угол NKB равен 45 град.
Тогда угол AKC 180-90-45 = 45 град.
Тогда угол KAC 180-90-45 = 45 град. Значит треугольник АКС прямоугольный равнобедренный и АС=СК и так как АК биссектриса, то СК=ВК и = АС.
Для прямоугольного треугольника АКС получаем
квадрат АК= квадрату АС + квадрат КС
квадрат АК = квадрат ВК + квадрат ВК
АК = ВК х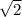
1 - 21 градусов
(180 градусов - 32 градуса) : 2= 74 градуса- углы А и С
74 градуса : 2= 37 градусов - угол А разделен биссектрисой АN
Рассмотрим прямоугольный треугольник AMC
90 градусов - 74 градуса= 16 градусов - угол MAC
угол NAC - угол MAC= 37 градусов - 16 градусов = 21 градус
2 - BR < AB < BT
угол Т= 30 градусов, поэтому катет, что находится напротив угла 30 градусов равен половине гипотенузы. В нашем случае BR=1/2 BT
Рассмотрим треугольник ABR. BR < AB так как гипотенуза всегда больше за катет.
Поэтому ответ BR < AB < BT