Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
а)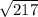
б)-28
Объяснение:
Чтобы найти координаты вектора XY для точек X(x1,x2,x3) и Y(y1,y2,y3) нужно переместить X в 0, т.е просто отнять x1 из y1 и т.д. Итого XY(y1-x1, y2-x2, y3-x3). Аналогично вычисляем:
AB(1-2,-2-4,3-5)=AB(-1,-6,-2)
BC(-1-1,-2-(-2),4-3)=BC(-2,0,1)
AC(-1-2,-2-4,4-5)=AC(-3,-6,1)
Вектор XY*k получается домножением каждой координаты на k, чтобы вычесть вектора нужно из координат первого вектора вычесть координаты второго вектора:
a=3AB-4AC=(3*(-1)-4*(-3),3*(-6)-4*(-6),3*(-2)-4*1)=(9,6,-10)
Длина вектора a - среднее квадратичное его координат:
|a|=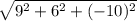 =
=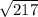
Формула скалярного произведения векторов a(a1,a2,a3) и b(b1,b2,b3) - ab=a1*b1+a2*b2+a3*c3
Итого ab=9*(-2)+6*0+(-10)*1=-28
ответ:В треугольной пирамиде проекция бокового ребра L на основание совпадает с отрезком, равным (2/3) высоты h треугольника в основании пирамиды.
h =(3/2)* (L*cos 60°) = (3/2)*(√3*(1/2)) = 3√3/4.
Сторона а основания равна:
а = h/cos 30° = (3√3/4)/(√3/2) = 3/2.
Высота пирамиды H = L*sin 60° = √3*(√3/2) = 3/2.
Основание пирамиды вписывается в шар по окружности радиуса Ro.
Ro = (1/3)h/(sin 30°) = (1/3)*(3√3/4)/(1/2) = √3/2.
Теперь переходим к рассмотрению осевого сечения пирамиды через два боковых ребра, развёрнутых в одну плоскость.
Для шара это будет диаметральное сечение.
Радиус шара Rш = (abc)/(4S).
Здесь a и b - боковые рёбра, с - диаметр описанной около основания пирамиды окружности (с = 2Ro = √3).
Сечение S = (1/2)H*(2Ro) = (1/2)*(3/2)*√3 = 3√3/4.
Получаем Rш = (√3*√3*√3)/(4*(3√3/4)) = 1.
Объём шара V = (4/3)πR³ = (4/3)π куб
Объяснение: