Даны точки А (2 ;2) В (6; 6). Пусть точка С- середина отрезка АВ. Составьте уравнение прямой, перпендикулярной прямой АВ и проходящей через точку С

Расстояния от середины гипотенузы до катетов это перпендикуляры опущенные на катеты из середины гипотенузы

Рассмотрим треугольник АМК (прямоугольный) и треугольник NKB (прямоугольный):

Они равны по стороне и двум прилежащим к ним углам.

Угол NBK = углу ANM как соответствующие при пересечении двум параллельных прямых СВ и MN третьей прямой АВ.

Угол MAN = углу KNB как соответствующие при пересечении двум параллельных прямых AC и NK третьей прямой АВ.

AN = NB из условия (АВ -гипотенуза).

Следовательно, треугольник АМК (прямоугольный) и треугольник NKB (прямоугольный) равны по второму признаку, то есть по стороне и двум прилежазщим к ней углам.

Следовательно, все стороны треугольника АМК соответственно равны сторонам треугольника NKВ. А, следовательно, АМ = NK = 8, MN = KB = 7.

Тогда АС = АМ + МС = 8+8=16.

          ВС = СК + КВ = 7+7=14.

Дальше найдем АВ по теореме пифагора, т. к. треугольник АСВ прямоугольный:

ответ: 14, 16,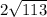

Точка касания с гипотенузой ВС является точка Е (СЕ=2, ВЕ=3), с катетом АС точка К, с катетом АВ точка М. Угол А прямой.

СЕ=СК=2, длины отрезков выходящих из одной вершины до точек касания к окружности равны, по этому же правилу

ВЕ=ВМ=3

Центр окружности О, r-радиус окружности. ОК=ОМ=r и ОК перепендик АС, ОМ перпендик АВ. АМОК-квадрат и АМ=АК=r

Тогда АС=r+2, АВ=r+3, ВС=2+3=5 по теореме Пифагора

ВС^2=АС^2+АВ^2

5^2=(r+2)^2+(r+3)^2

r^2+4r+4+ r^2+6r+9=25

2r^2+10r+13=25

2r^2+10r-12=0 сократим все на 2

r^2+5r-6=0

найдем дискрим. Д=25+24=49

корень из Д=7

r1=(-5+7)/2

r1=1

r2=(-5-7)/2=-6(радиус не может быть отрицательным)

Радиус вписан.окружности равен r=1см