ОВ=ОС=R, ОА - общая, АВ=АС (по определению - отрезки касательных, проведенных из одной точки, равны) => эти треугольники равны по 3-му признаку=> уголВОА=угол ОСА.
Рассм. треуг. АОВ: т.к. ОВ в 2 раза меньше АО, то угол ОАВ=30 градусов(сторона, лежащая напротив угла в 30 градусов, равна половине гипотенузы). угол ВОА=180-90-30=60 градусов.
Дано: АВ и АС - касательные, ОА=30 см, ОВ=15 см.
Найти: угол ВОС.
Рассмотрим треуг-ки АОВ и АОС:
ОВ=ОС=R, ОА - общая, АВ=АС (по определению - отрезки касательных, проведенных из одной точки, равны) => эти треугольники равны по 3-му признаку=> уголВОА=угол ОСА.
Рассм. треуг. АОВ: т.к. ОВ в 2 раза меньше АО, то угол ОАВ=30 градусов(сторона, лежащая напротив угла в 30 градусов, равна половине гипотенузы). угол ВОА=180-90-30=60 градусов.
угол ВОС= угол ВОА+ угол ОСА= 60+60=120 градусов.
ответ: 120 градусов.
5. 28
6. 21
Объяснение:
5. АВ = 42, 2BC = AC - это если наше условие написать на математическом языке. Чтобы решить эту задачу, нужно составить уравнение
AC + BC = 42
Но чтобы у нас не было двух неизвестных, нужно один отрезок выразить через другой. Для этого мы и переписали условие
АС + BC = 2BC + BC
2BC + BC = 42
3BC = 42
BC = 42 : 3 = 14
Если BC = 14, то АС = 42 - 14 = 28.
6. АВ = 49, АС =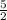
CB или 2,5СВ
Чтобы найти АС, мы переписали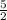
в 2,5 , чтобы проще было посчитать. АС - это две части и одна половинка этой части СВ. То есть,
СВ + СВ +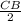
= AC.
СВ + СВ +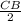
+ СВ = 49
3СВ +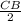
= 49, чтобы легко избавиться от некрасивой дроби, нужно две части уравнения домножить на 2
6СВ + СВ = 98
7СВ = 98
СВ = 14, следовательно АС = 49 - 14 = 35
Раз нам надо найти АС - СВ, то 35 - 14 = 21.