1) отрезки, на которые биссектриса делит боковую сторону, равны 8*x и a*x, где а - неизвестное основание, x тоже неизвестен. Зато известно вот что: a/2 = 8/(8*x); a/2 = 1/x; 8*x + a*x = 8; 1/x = 1 + a/8; Отсюда a/2 = 1 + a/8; a = 8/3; высота h треугольника находится так h^2 = 8^2 - (a/2)^2; h = (4/3)*√35; Площадь S = (1/2)*(8/3)*(4/3)*√35 = (16/9)*√35; 2) В равнобедренной трапеции проекция диагонали на большее основание равна средней линии (а второй отрезок, на который высота из вершины меньшего основания делит большее, то есть - проекция боковой стороны на основание - равен полуразности оснований, докажите самостоятельно, это элементарно). Поэтому высота, средняя линяя и диагональ образуют прямоугольный треугольник, произведение катетов которого рано 48, а сумма квадратов равна 10^2; m^2 + h^2 = 10^2; m*h = 48; Отсюда (m + h)^2 = 196; (m - h)^2 = 4; Если m > h, то m + h = 14; m - h = 2; h = 6; m = 8; Если m > h, то m + h = 14; h - m = 2; h = 8; m = 6; то есть - два решения h = 6 или 8; ответ можно было бы увидеть сразу, поскольку "египетский" треугольник 6,8,10 удовлетворяет условию.
Т.к. один его угол равен 30°, то второй угол = 180 - 90 = 60, т.е. это прямоугольный треугольник 30 60 90, а по его свойству, катет, противолежащий углу 30° (AD) равен половине гипотенузы (BD), т.е. гипотенуза BD равна:
BD = 2*AD = 2*12 = 24,
а катет, прилежащий углу 30° (AB) равен от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
Итак:
AB = 12 ;
Объем параллелепипеда равен произведению его сторон:
a/2 = 8/(8*x); a/2 = 1/x;
8*x + a*x = 8; 1/x = 1 + a/8;
Отсюда a/2 = 1 + a/8; a = 8/3; высота h треугольника находится так
h^2 = 8^2 - (a/2)^2; h = (4/3)*√35; Площадь S = (1/2)*(8/3)*(4/3)*√35 = (16/9)*√35;
2) В равнобедренной трапеции проекция диагонали на большее основание равна средней линии (а второй отрезок, на который высота из вершины меньшего основания делит большее, то есть - проекция боковой стороны на основание - равен полуразности оснований, докажите самостоятельно, это элементарно).
Поэтому высота, средняя линяя и диагональ образуют прямоугольный треугольник, произведение катетов которого рано 48, а сумма квадратов равна 10^2;
m^2 + h^2 = 10^2;
m*h = 48;
Отсюда
(m + h)^2 = 196;
(m - h)^2 = 4;
Если m > h, то m + h = 14; m - h = 2; h = 6; m = 8;
Если m > h, то m + h = 14; h - m = 2; h = 8; m = 6;
то есть - два решения h = 6 или 8;
ответ можно было бы увидеть сразу, поскольку "египетский" треугольник 6,8,10 удовлетворяет условию.
V = 720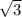
≈ 1247,0766
Объяснение:
Треугольник ABD - прямоугольный.
Т.к. один его угол равен 30°, то второй угол = 180 - 90 = 60, т.е. это прямоугольный треугольник 30 60 90, а по его свойству, катет, противолежащий углу 30° (AD) равен половине гипотенузы (BD), т.е. гипотенуза BD равна:
BD = 2*AD = 2*12 = 24,
а катет, прилежащий углу 30° (AB) равен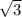
от противолежащего углу катета (AD), что доказывается теоремой Пифагора:
Итак:
AB = 12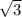
;
Объем параллелепипеда равен произведению его сторон:
V = AA1 * AD * AB = 5 * 12 * 12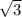
= 720