Зная 2 стороны и угол между ними, мы можем найти третью сторону — по теореме косинусов.
Косинус бетты мы найдём по её синусу:
β = 45°.
Теперь, чтобы найти третью сторону — используем теорему косинусов:
Теперь, зная все стороны треугольника, найдём площадь — по теореме Герона:
Вывод: S = 20.56.
2.
Для вычисления синуса альфы, нам потребуется знать косинус альфы, а для вычисления этого же косинуса, нам и сторон достаточно — используем теорему косинусов:
Этим следует:
Вывод: sinα = 0.92.
3.
Найдём синус гаммы:
Формула вычисления площади, через 2 стороны и синус — такова:
Всё решение в файле. Верно заметили товарищи модераторы, что я рассматривал частный случай. Решаем для общего: Соединяем концы хорд с центром окружности, получаем 2 треугольника. 1)Радиусы равны в любом случае, еще дано равенство хорд, значит, треугольники равны по 3 сторонам. Равноудаленность показывают равные высоты а если треугольники равны, то равны и их соответственные элементы, к высотам это так же относится. Ч.т.д. 2)Радиусы по-прежнему равны. Здесь рассматриваем уже прямоугольные треугольники, на которые разбивают высоты наших треугольников (они же биссектрисы и медианы в связи с тем, что треугольники равнобедренные). Получается, что все 4 треугольника равны между собой по гипотенузе (радиус) и катету (высоте), а значит, что и "большие" треугольники равны между собой, т.к. составляющие их геометрические фигуры соответственно равны. А это, в свою очередь, значит, что в этих треугольниках все соответственные элементы равны, в том числе и хорды окружности, ч.т.д.
1.
Зная 2 стороны и угол между ними, мы можем найти третью сторону — по теореме косинусов.
Косинус бетты мы найдём по её синусу:
β = 45°.
Теперь, чтобы найти третью сторону — используем теорему косинусов:
Теперь, зная все стороны треугольника, найдём площадь — по теореме Герона:
Вывод: S = 20.56.
2.
Для вычисления синуса альфы, нам потребуется знать косинус альфы, а для вычисления этого же косинуса, нам и сторон достаточно — используем теорему косинусов:
Этим следует:
Вывод: sinα = 0.92.
3.
Найдём синус гаммы:
Формула вычисления площади, через 2 стороны и синус — такова: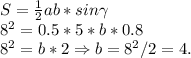
Вывод: AC = 4.
Верно заметили товарищи модераторы, что я рассматривал частный случай. Решаем для общего:
Соединяем концы хорд с центром окружности, получаем 2 треугольника.
1)Радиусы равны в любом случае, еще дано равенство хорд, значит, треугольники равны по 3 сторонам. Равноудаленность показывают равные высоты а если треугольники равны, то равны и их соответственные элементы, к высотам это так же относится. Ч.т.д.
2)Радиусы по-прежнему равны. Здесь рассматриваем уже прямоугольные треугольники, на которые разбивают высоты наших треугольников (они же биссектрисы и медианы в связи с тем, что треугольники равнобедренные). Получается, что все 4 треугольника равны между собой по гипотенузе (радиус) и катету (высоте), а значит, что и "большие" треугольники равны между собой, т.к. составляющие их геометрические фигуры соответственно равны. А это, в свою очередь, значит, что в этих треугольниках все соответственные элементы равны, в том числе и хорды окружности, ч.т.д.