По признаку параллельности прямых, если внутренние накрест лежащие углы при прямых а и b и секущей с равны, то эти прямые параллельны. Значит, прямые а и b параллельны. Это раз.
Второе. Из условия параллельности прямых а и в вытекает равенство углов 3 и 5, которые тоже будут внутренними накрест лежащими уже при параллельных а и b и секущей с, и уже по свойству параллельных прямых a и b и секущей с следует ∠3=∠5
2)∠2=∠6, ∠1=∠5; ∠4=∠8; ∠3=∠7- указаны пары соответственных углов при параллельных а и b и секущей с. Поэтому по свойству соответственных углов данные углы равны.
3) ∠4+∠5=180°; ∠3+∠6=180°, это сумма внутренних односторонних при параллельных а и b и секущей с. Сумма их равна 180° по свойству внутр. односторонних.
Подводим итог. Сначала доказали параллельность прямых а и b при секущей с по признаку параллельности прямых, а затем для решения 1),2),3) воспользовались свойствами указанных углов при параллельных прямых а и b и секущей с.
По признаку параллельности прямых, если внутренние накрест лежащие углы при прямых а и b и секущей с равны, то эти прямые параллельны. Значит, прямые а и b параллельны. Это раз.
Второе. Из условия параллельности прямых а и в вытекает равенство углов 3 и 5, которые тоже будут внутренними накрест лежащими уже при параллельных а и b и секущей с, и уже по свойству параллельных прямых a и b и секущей с следует ∠3=∠5
2)∠2=∠6, ∠1=∠5; ∠4=∠8; ∠3=∠7- указаны пары соответственных углов при параллельных а и b и секущей с. Поэтому по свойству соответственных углов данные углы равны.
3) ∠4+∠5=180°; ∠3+∠6=180°, это сумма внутренних односторонних при параллельных а и b и секущей с. Сумма их равна 180° по свойству внутр. односторонних.
Подводим итог. Сначала доказали параллельность прямых а и b при секущей с по признаку параллельности прямых, а затем для решения 1),2),3) воспользовались свойствами указанных углов при параллельных прямых а и b и секущей с.
B2. Дан ΔABC, точка M — середина стороны AB, точка N — середина стороны BC,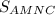
= 60. Найти 
.
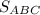MN || AB, MN =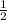
AB ⇒ ∠BMN = ∠BAC ⇒ ΔBMN подобный ΔBAC.
ответ: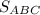
= 80 ед. кв.
B3. AK — биссектриса ΔABC, АВ = 4, ВК = 2, КС = 3. Найти периметр ΔABC.
Биссектриса угла делит противоположную сторону на отрезки, пропорциональные прилегающим сторонам:
P = AB+AC+(BK+CK)
P = 4+6+(2+3) = 15
ответ: Периметр ΔАВС равен 15.
B4. Площадь прямоугольного ΔABC равна 360 см², АС:ВС = 3:4. Из середины гипотенузы восстановлен перпендикуляр КМ. Найти площадь ΔMKC.
BK = CK =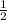
BC
∠ABC = ∠KMC ⇒ ΔCKM и ΔCAB подобны по двум углам и пропорциональной стороне.
ответ: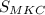
= 160 см².