Осевое сечение АВС конуса есть равнобедренный треугольник с углом при вершине С равным 1200. Высота ОС конуса, есть высота, биссектриса и медиана треугольника АВС, тогда угол АСО = АСВ / 2 = 120 / 2 = 600.
В прямоугольном треугольнике АОС, через угол и катет определим длину гипотенузы и второго катета.
Cos60 = ОС / АС.
АС = ОС / Cos60 = 12 / (1 / 2) = 24 см
tg60 = AO / OC.
AO = OC * tg60 = 12 * √3 см.
Определим площадь основания конуса.
Sосн = п * R2 = п * 432 см2.
Определим площадь боковой поверхности конуса.
Sбок = п * R * L = п * АО * АС = п * 12 * √3 * 24 = п * 288 * √3 см2.
Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.
Объяснение:
АВ* РВ=СB*МB /: СВ*РВ ,
, .
По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника ( ) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС
Осевое сечение АВС конуса есть равнобедренный треугольник с углом при вершине С равным 1200. Высота ОС конуса, есть высота, биссектриса и медиана треугольника АВС, тогда угол АСО = АСВ / 2 = 120 / 2 = 600.
В прямоугольном треугольнике АОС, через угол и катет определим длину гипотенузы и второго катета.
Cos60 = ОС / АС.
АС = ОС / Cos60 = 12 / (1 / 2) = 24 см
tg60 = AO / OC.
AO = OC * tg60 = 12 * √3 см.
Определим площадь основания конуса.
Sосн = п * R2 = п * 432 см2.
Определим площадь боковой поверхности конуса.
Sбок = п * R * L = п * АО * АС = п * 12 * √3 * 24 = п * 288 * √3 см2.
Тогда Sпов = Sосн + Sбок = п * 432 + п * 288 * √3 = 144 * (3 + 2 * √3) см2.
ответ: Площадь поверхности конуса равна 144 * (3 + 2 * √3) см2.
Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.
Объяснение:
АВ* РВ=СB*МB /: СВ*РВ ,
По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника (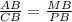
) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС