Точка Е делит отрезок DF на два отрезка. Если известно, что DF=24 см и что отрезок FE в 3 раза длиннее DE, найдите длины отрезков DE и FE. НАЗНАЧУ КАК ХА ЛУЧШИЙ
Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть .
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда .
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой координаты точки А(4,3) и , например, В(2,0), получим:
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
1. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-47°=43°
Відповідь: 43°
2. Знайдемо суміжний кут зовнішнього кута 180°-117°=63°. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-63°=27°
Відповідь: 63° та 27°
3. В цій задачі скористаємося теоремою Піфагора, щоб знайти другий катет:
см
4. Оскільки із означення вписаного в коло прямокутного трикутника відомо, що радіус описаного кола дорівнює половині гіпотенузи, то гіпотенуза в даній задачі дорівнює відомому катету збільшеному в д рази.
Знайдемо кут протилежний відомому катету х:
Один кут = 30°. Оскільки це прямокутний трикутник, то прямий кут = 90°, а третій кут = 180°-90°-30°=60°
Відповідь: кути трикутника 30°, 60°, 90°
5. Оскільки дотична із радіусом утворюють кут 90°, то утворюється прямокутний трикутник АОМ, в якому потрібно знайти гіпотенузу ОМ.
Третій кут в трикутнику буде дорівнювати 60°, оскільки 180°-90°-30°=60°.
Рассмотрим вариант, когда прямая имеет угловой коэффициент k>0, тогда она наклонена к положительному направлению оси ОХ под острым углом. Из чертежа видно, что угол наклона не может быть тупым, т.к. тогда S треугольника будет больше 3 .
От координатного угла отсекается ΔВОК , площадь которого S=3. Это прямоугольный треугольник, его площадь равна половине произведения катетов., то есть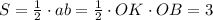 .
.
Пусть ОК=3 ед. , а ОВ=2 ед. , тогда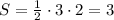 .
.
Точка В в этом случае будет иметь координаты В(2,0), а точка К(0,-3) .
Подставим в уравнение прямой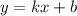 координаты точки А(4,3) и , например, В(2,0), получим:
координаты точки А(4,3) и , например, В(2,0), получим:
Или можно использовать то, что точка пересечения с осью ОУ имеет координаты К(0,-3). Тогда уравнение прямой имеет вид: y=kx-3 . И в это уравнение уже подставить координаты точки А(4,3) :
Также можно было составить уравнение прямой, проходящей через две точки А и В ( или А и К) .
Смотри рисунок.
Відповідь:
Пояснення:
1. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-47°=43°
Відповідь: 43°
2. Знайдемо суміжний кут зовнішнього кута 180°-117°=63°. В прямокутному трикутнику один з кутів = 90°, а сума всіх кутів = 180°. Виходячи з цього невідомий кут х=180°-90°-63°=27°
Відповідь: 63° та 27°
3. В цій задачі скористаємося теоремою Піфагора, щоб знайти другий катет:
4. Оскільки із означення вписаного в коло прямокутного трикутника відомо, що радіус описаного кола дорівнює половині гіпотенузи, то гіпотенуза в даній задачі дорівнює відомому катету збільшеному в д рази.
Знайдемо кут протилежний відомому катету х:
Один кут = 30°. Оскільки це прямокутний трикутник, то прямий кут = 90°, а третій кут = 180°-90°-30°=60°
Відповідь: кути трикутника 30°, 60°, 90°
5. Оскільки дотична із радіусом утворюють кут 90°, то утворюється прямокутний трикутник АОМ, в якому потрібно знайти гіпотенузу ОМ.
Третій кут в трикутнику буде дорівнювати 60°, оскільки 180°-90°-30°=60°.
За теоремою Синусів