Точки a и b делят окружность с центром o на дуги amb и acb так, что дуга acb на 400 меньше дуги amb. am – диаметр окружности. найдите углы amb, abm, acb. если можно, с рисунком)

Показать ответ

Ответ:

lozinskayaeliz

09.02.2022 17:23

ответ: S = 90

Объяснение:

Сделаем дополнительные построения (на рисунке).

Из треугольника EFD найдем высоту DF.

DF²= ED²-EF² = 117 - 81 = 36 и отсюда DF = 6

В новом параллелограмме BEDF диагонали пересекаются и делятся пополам, значит ОЕ = OF = EF/2 = 4,5

Из треугольника ОFD по Пифагору найдем OD

OD² = OF² + FD² = 4,5²+6² = 56,25 и тогда OD = 7,5

Но диагонали прямоугольника равны и в точке пересечения делятся пополам, то есть АС=BD = 7,2*2 = 15

Теперь найдем синус угла между диагоналями <FOD из того же треугольника OFD

sin(FOD) = ED/OD = 6/7.5 =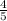 $\frac{4}{5}$

S = 0,5*AC*BD*sin(FOD) = 0,5*15*15*4/5 = 90

0,0(0 оценок)

Ответ:

Ryuuko

21.01.2020 12:09

Доброго времени суток!

Как я поняла, вопрос был поставлен таков : "Стороны равнобедренного треугольника пропорциональны числам 1, 1, √2. Докажите, что этот треугольник — прямоугольный".

если это не так, то сообщите об этом в комментариях.

▔ ▔ ▔

★☆★ Чертёж смотрите во вложении ★☆★

Дано:

ΔАВС — равнобедренный (АВ = ВС).

АВ : ВС : АС = 1 : 1 : √2.

Доказать:

ΔАВС — прямоугольный.

Доказательство:

▸Теорема, обратная теореме Пифагора — если квадрат большей стороны треугольника равен сумме квадратов других сторон, то такой треугольник — прямоугольный◂

Итак, пусть АВ = ВС = х, тогда, по условию задачи, АС = х√2.

Составим уравнение и проверим его на верность —

$x^{2} +x^{2} =(x\sqrt{2} )^{2} \\\\2x^{2} = x^{2} \sqrt{2^{2}} \\\\\boxed{ 2x^{2} =2x^{2} }$

Итак, мы выяснили, что сумма квадратов меньших сторон равна квадрату большей стороны. Поэтому, по обратной теореме Пифагора, равнобедренный ΔАВС — прямоугольный.

ответ:

что требовалось доказать.