Геометрия: Тов; а) /4 ас ZID = 54)2 = 4°, L5 - 150°И) 24-е - ДВ : 2 а.2)24-bot Co. A = 60-а2)

Тов; а) /4 ас ZID = 54
)2 = 4°, L5 - 150°
И) 24-е - ДВ : 2 а.
2)24-bot Co. A = 60-а
2)

Показать ответ

Ответ:

Мен234

16.12.2020 23:38

Ребро не было указано в условии задачи, поэтому я обозначу его за {a}.

--------------

а)

проекция Точки A на плоскость (A1B1C1)=A1, проекция точки D=D1, значит проекция отрезка AD=A1D1.

Отрезок A1D1║B1C1 из свойств правильного шестиугольника, и A1D1║AD так как плоскость (ABC)║(A1B1C1) значит AD║B1C1 Ч.Т.Д.

---------------

б)

Рассмотрим треугольник A1B1C1, опустим высоту A1H на основание B1C1, AH Также будет ⊥B1C1 по теореме о трех перпендикулярах, значит AH искомое расстояние.

AA1 будет ⊥A1H так-как он ⊥ плоскости (A1B1C1).

найдем A1H методом площадей в треугольнике A1B1C1.

$S=\frac{1}{2} A_1B_1*B_1C_1*sin(120)=\frac{1}{2} B_1C_1*A_1H\\a^2*sin(120)=a*A_1H\\A_1H=a*sin(180-60)=a*sin(60)=\frac{a\sqrt{3}}{2}$

A1H также можно было найти рассмотрев треугольник A1BH, сказав что A1H=A1B1*sin(60)

-----------

теперь по теореме пифагора найдем AH:

$AH=\sqrt{A_1H^2+AA_1^2}=\sqrt{\frac{4a^2}{4}+\frac{3a^2}{4}}=\frac{a\sqrt{7}}{2}$

ответ: $AH=\frac{a\sqrt{7}}{4}$

Вправильной шестиугольной призме abcdefa1b1c1d1e1f1 , все ребра равны. а) докажите, что прямые ad и

0,0(0 оценок)

Ответ:

verunyabogachk

23.02.2021 12:45

Так как 120 тупой угол, то он образует большую сторону, соответственно он не относится к треугольнику с 10 см.

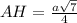
Узнаем второй угол, который образуют диагонали прямоугольника:

360-(120+120)=120 градусов - углы образованные диагоналями вместе

120/2=60 градусов - угол образованный диагоналями (острый соответственно подходит)

Диагонали прямоугольника равны и делят друг друга пополам, соответственно треугольник с углом 60 градусов равнобедренный. Узнаем остальные углы:

180-60=120 градусов - углы при основании вместе.

120:2=60 градусов - углы при основании (каждый)

Выходит, что все углы равны 60 градусов, соответственно треугольник равносторонний, а так как одна его сторона равна 10 см, то 10 см равны все его стороны.
Соответственно половина диагонали равна 10 см, умножаем 10 на 2, выходит 20 см.

ответ: C

0,0(0 оценок)

Популярные вопросы: Геометрия