У ромбі ABCD з вершини тупого кута B проведені висоти ВЕ і ВF до сторін AD і DC відповідно. Кут EBF дорівнює 30°. Знайдіть периметр ромба, якщо ВЕ = 6 см.
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 11 см, інше коло має бути радіусом (R2) більшим або рівним 10 см ( |R1−d| ) і меншим за 32 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
10 ≤ R2 ≤ 32
Коло з радіусом 37 в даний інтервал довжин не входить, нерівність не виконується ⇒ спільних точок немає.
б)
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 37 см, інше коло має бути радіусом (R2) більшим або рівним 16 см ( |R1−d| ) і меншим за 58 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
16 ≤ R2 ≤ 58
Коло з радіусом 37 в даний інтервал довжин входить, нерівність строга ⇒ спільних точок дві.
а)
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 11 см, інше коло має бути радіусом (R2) більшим або рівним 10 см ( |R1−d| ) і меншим за 32 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
10 ≤ R2 ≤ 32
Коло з радіусом 37 в даний інтервал довжин не входить, нерівність не виконується ⇒ спільних точок немає.
б)
У випадку, коли радіус першого кола R1 = 21 см і відстань до центру другого d = 37 см, інше коло має бути радіусом (R2) більшим або рівним 16 см ( |R1−d| ) і меншим за 58 ( |R1+d| ). Якщо виконується строга нерівність, то точок перетину буде дві; якщо виконується нестрога нерівність, точка перетину одна — дотична; якщо нерівність не виконується, друге коло не перетинає перше.
16 ≤ R2 ≤ 58
Коло з радіусом 37 в даний інтервал довжин входить, нерівність строга ⇒ спільних точок дві.
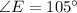
Объяснение:Проведём биссектрисы
и 
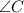. Пусть они пересекаются в точке 
.
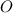Также проведём отрезки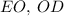
и 
.
========================================
Рассмотрим
:
Сумма внутренних углов треугольника равна
.
========================================
Рассмотрим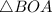
и 
:
========================================
Рассмотрим
и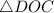 
:
========================================
========================================
Рассмотрим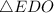
:
========================================
Рассмотрим геометрическую фигуру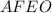
:
При пересечении двух параллельных прямых секущей, сумма односторонних углов равна
.
Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.
У параллелограмма противоположные углы равны.
========================================