У сектор радіуса R з центральним кутом 60° вписано два кола, які дотикаються одне одного, і радіусів, що обмежують сектор. Знайдіть відношення довжин цих кіл, якщо радіус одного з них на 4 см більший за радіус другого. Чому дорівнює R?
Площадь полной поверхности прямоугольного параллелепипеда
равна сумме площадей 6 прямоугольников, его образующих.
Площадь двух прямоугольников, со сторонами 6 и 12 = 6*12 = 72 кв.ед
Обозначим третью сторону параллелепипеда за x, тогда
S(полн. пов) = 2(72+6x+12x)
2(72+6x+12x) = 576
144 + 36х = 576
36х = 432
x = 12
Длина диагонали прямоугольного параллелепипеда равна корню суммы квадратов трёх его измерений.
d =
Предположим, что мы не знаем данное свойство, тогда мы найдём диагональ основания параллелепипеда со сторонами 6 и 12 исходными. Т.к, параллепипед прямоугольный, то по теореме Пифагора следует, что
d1 = . Можно не считать, а пока оставить так.
Найдём теперь диагональ параллелепипеда. Найденная диагональ является проекцией диагонали параллелепипеда на его основание.
Чтобы её найти, мы берём третью сторону (высоту параллелепипеда) и найденную диагональ. Также, по т. Пифагора находим диагональ параллелепипеда d2
Объяснение:
Пусть ВС-малое основание, а AD-большое. т.О -пересечение диагоналей.
<AOD=180-26=154
Тр-к AOD-р/б,т.к. углы при основании равны. Отсюда <CAD=<BDA=(180-154)/2=13.
Вписанный угол в 2 раза меньше дуги на которую опирается.
<CAD-вписанный и опирается на дугу, описанной окружности CD. Отсюда дуга CD=2*13=26
<BDA-вписанный и опирается на дугу, описанной окружности AB. Отсюда дуга AB=2*13=26
Трапеция лежит на диагонали,поэтому нас интересует только полуокружность.
Дуга ВС=180-(26+26)=128
<BAC=<BDC=128/2=64
<A=<D=64+13=77
BC||AD (по св-ву трапеции), <A+<B=180
<B=<C=180-77=103
Площадь полной поверхности прямоугольного параллелепипеда
равна сумме площадей 6 прямоугольников, его образующих.
Площадь двух прямоугольников, со сторонами 6 и 12 = 6*12 = 72 кв.ед
Обозначим третью сторону параллелепипеда за x, тогда
S(полн. пов) = 2(72+6x+12x)
2(72+6x+12x) = 576
144 + 36х = 576
36х = 432
x = 12
Длина диагонали прямоугольного параллелепипеда равна корню суммы квадратов трёх его измерений.
d =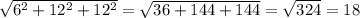
Предположим, что мы не знаем данное свойство, тогда мы найдём диагональ основания параллелепипеда со сторонами 6 и 12 исходными. Т.к, параллепипед прямоугольный, то по теореме Пифагора следует, что
d1 =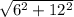 . Можно не считать, а пока оставить так.
. Можно не считать, а пока оставить так.
Найдём теперь диагональ параллелепипеда. Найденная диагональ является проекцией диагонали параллелепипеда на его основание.
Чтобы её найти, мы берём третью сторону (высоту параллелепипеда) и найденную диагональ. Также, по т. Пифагора находим диагональ параллелепипеда d2
d2 =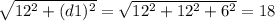
Отсюда и вытекает свойство о трёх измерениях.
ОТВЕТ: 18