Дано: Хорды AB=CD пересекаются в точке О. Доказать: AO=CO, DO=BO.
Док-во: Соединим точки A B C D как на рисунке и рассмотрим треугольники ABD и CDB. Равные хорды стягивают равные дуги, значит вписанные углы ADB и CBD равны, а вписанные углы DAB и BCD опираются на одну и ту же дугу, значит они равны. Поскольку в треугольнике сумма углов равна 180°, то и оставшиеся углы ABD и CDB равны. Из равенства этих двух углов (<ABD=<CDB) следует, что △DOB - равнобедренный. => DO=BO. Поскольку AB=AO+BO и CD=DO+CO, а AB=CD, то и AO=CO, чтд.
Объяснение:
Дано: Хорды AB=CD пересекаются в точке О. Доказать: AO=CO, DO=BO.
Док-во: Соединим точки A B C D как на рисунке и рассмотрим треугольники ABD и CDB. Равные хорды стягивают равные дуги, значит вписанные углы ADB и CBD равны, а вписанные углы DAB и BCD опираются на одну и ту же дугу, значит они равны. Поскольку в треугольнике сумма углов равна 180°, то и оставшиеся углы ABD и CDB равны. Из равенства этих двух углов (<ABD=<CDB) следует, что △DOB - равнобедренный. => DO=BO. Поскольку AB=AO+BO и CD=DO+CO, а AB=CD, то и AO=CO, чтд.
1)гипотенуза=
=13см ( по т. Пифагора)
2)катет=
=8 см
3)В ромбе диагонали точкой пересечения делятся пополам и пересекаются под прямым углом, следовательно получаем
1катет=6 см, 2катет=8 см
сторона=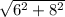
=10cм
4)Т.е. нужно найти катет из треуг. с гипотенузой 10 см и катетом 16:2=8см
2 катет=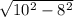
=6cм
ТОгда диагональ = 6*2=12см
5)S=a*b*sin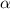
S=16*12*0,5=96cм^2
6)1/2 основания =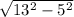
=12cМ
Основание треуг.=12*2=24см
S=0,5*24*5=60cм^2
7) Высота=
=12см
S=a*ah=20*12=240cм^2
8)Высота СН=АВ=10см
треуг. DНС-р/б
НD=HC=10cМ
ВС=18-10=8см
S=(18+8)/2*10=130см^2