1. полупериметр 50/2=25, одна из сторон АВ=СD=10cм⇒две другие BC=AD=25-10=15/см/
ответ 10 см, 15 см.
2. задача задана некорректно, если угол А равен 36° , то угол В равен 90°, т.к. угол С равен 117°, но угол С равен не 117°, а 90°, и тогда угол D равен 117°. Если бы в задаче была трапеция АВDС, то корректность условия была бы налицо.
Если бы не было именованных сторон, т.е. указали бы два угла острый и тупой, но даже если бы выполнялись эти все условия. задача все равно некорректна, т.к. сумма углов четырехугольника равна 360°, два угла прямых, это 180°, а сумма двух других 117°+36°≠180°
3. периметр - это сумма всех сторон. у квадрата они равны. поэтому периметр равен 4*4=16/см/
4. Т.к. ∠В=60°, то в ΔАВС углы А и С тоже по 60°, ΔАВС- равносторонний. т.е. сторона ромба равна диагонали АС, 10.5см, а его периметр 10.5*4=42/см/
5. О- точка пересечения диагоналей. т.к. диагонали параллелограмма, пересекаясь, делятся точкой пересечения пополам, поэтому противолежащие вершины параллелограмма находятся на одинаковом расстоянии от точки пересечения диагоналей, а потому О- центр симметрии. Доказано.
1. полупериметр 50/2=25, одна из сторон АВ=СD=10cм⇒две другие BC=AD=25-10=15/см/
ответ 10 см, 15 см.
2. задача задана некорректно, если угол А равен 36° , то угол В равен 90°, т.к. угол С равен 117°, но угол С равен не 117°, а 90°, и тогда угол D равен 117°. Если бы в задаче была трапеция АВDС, то корректность условия была бы налицо.
Если бы не было именованных сторон, т.е. указали бы два угла острый и тупой, но даже если бы выполнялись эти все условия. задача все равно некорректна, т.к. сумма углов четырехугольника равна 360°, два угла прямых, это 180°, а сумма двух других 117°+36°≠180°
3. периметр - это сумма всех сторон. у квадрата они равны. поэтому периметр равен 4*4=16/см/
4. Т.к. ∠В=60°, то в ΔАВС углы А и С тоже по 60°, ΔАВС- равносторонний. т.е. сторона ромба равна диагонали АС, 10.5см, а его периметр 10.5*4=42/см/
5. О- точка пересечения диагоналей. т.к. диагонали параллелограмма, пересекаясь, делятся точкой пересечения пополам, поэтому противолежащие вершины параллелограмма находятся на одинаковом расстоянии от точки пересечения диагоналей, а потому О- центр симметрии. Доказано.
Пусть S₁ - это площадь бо́льшего треугольника, а S₂ - площадь меньшего треугольника.
Пусть k > 1 (это значит, что в числителе будет стоять бо́льший треугольник).
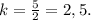
Площади подобных треугольников относятся как квадрат коэффициента подобия.Отсюда -
1,28 (ед²).
- - -
Случай 2 - Площадь меньшего треугольника равна 8 (ед²).В этом случае наоборот k < 1 (в числителе будет стоять меньший треугольник).
S₁ - площадь бо́льшего треугольника, S₂ - площадь меньшего треугольника
Тогда -
50 (ед²).