В прямоугольном треугольнике острый угол относится к внешнему, не смежному с ним как 4 10 . Найдите острые углы тнеугольника и его гипотенузу , если катет, лежащий напротив наименьшего острого угла равен 8 см

На рисунке изображена прямоугольная трапеция ABCD, в которую вписан круг. Точка касания окружности делит большую боковую сторону на отрезки длиной 4 см и 25 см. Установите соответствие между началом предложения (1 - 4) и его окончанием (а-д) так, чтобы образовалось правильное утверждение

1 Средняя линия трапеции равна ,2 Высота трапеции равна , 3 радиус вписанной окружности равен , 4 Меньшая диагональ трапеции равна

A )√ 594 см , Б) 20 см, В)2√149 см , Г) 10 см , Д) 24,5 см

Объяснение:

1) Найдем радиус вписанной окружности r=√(CH*HD)=√(4*25)10 (cм)⇒

диаметр ,равный высоте трапеции , равен 2*10=20( см), h=20 cм.

2)Высота прямоугольной трапеции равна меньшей боковой стороне ⇒ АВ=20 см.

3)Суммы противоположных сторон любого четырёхугольника описанного около окружности равны :  АВ+CD=BC+AD ⇒BC+AD=20+29=49 (см)

По определению средней линии трапеции имеем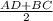  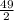 = =24,5(см)

4) Меньшей диагональю будет АС.

По свойству отрезков касательных СН=СК=4 см, ВМ=ВК=10 см, тогда ВС=4+10=14 (см)

ΔАВС-прямоугольный по т. Пифагора АС=√(14²+20²)=√596=√(4*149)=2√149 ( см).

ответ .   1-Д   ; 2-Б    ; 3-Г  ; 4-В .

Вписанные углы опирающиеся на диаметр равны по 90°, поэтому ∠ADC=90°=∠CBA.

Треугольник ADC - равнобедренный (DA=DC) и прямоугольный (∠ADC=90°), поэтому углы при его основании равны по 45°. ∠DAC=45°=∠DCA

Треугольник ABC - прямоугольный (∠CBA=90°), так же 2AB=AC. Угол лежащий напротив катета, который вдвое меньше гипотенузы равен 30°, поэтому ∠BCA=30°. Сумма острых углов в прямоугольном треугольнике составляет 90°, поэтому ∠BАС=60°.

∠BAD = ∠BAC+∠DAC = 60°+45° = 105°

∠BCD = ∠BCA+∠DCA = 30°+45° = 75°

ответ: ∠BAD=105°; ∠BСD=75°.