Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:
см
см
Площа прямокутного трикутника знаходится як півдобуток його катетів:
см²
Другий б
Висота прямокутного трикутника, що проведена до гіпотенузи з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
см
Площа будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи і висоти , що до неї проведена:
Объяснение: так как данный треугольник равнобедренный, то высота проведённая к основанию является ещё и медианой и делит основание на два равных прямоугольных треугольников. Рассмотрим один из них. Боковая сторона в полученном треугольнике является гипотенузой, а высота - катетом. Вычислим второй катет по теореме Пифагора:
25²- 15²=√(625-225)=√400=20
Этот катет равен половине основания данного треугольника, и поэтому его основание = 20×2=40см.
Основание= 40см
Теперь найдём площадь треугольника по формуле: ½×а×h, где h - его высота, "а"- сторона, к которой проведена высота:
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою і проекцією цього катета на гіпотенузу:
і проекцією цього катета на гіпотенузу:
Площа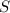 прямокутного трикутника знаходится як півдобуток його катетів:
прямокутного трикутника знаходится як півдобуток його катетів:
Другий б
Висота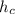 прямокутного трикутника, що проведена до гіпотенузи
прямокутного трикутника, що проведена до гіпотенузи  з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
Площа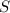 будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи
будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи  і висоти
і висоти 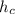 , що до неї проведена:
, що до неї проведена:
Відповідь: 180 см².
ответ: S=300см²
Объяснение: так как данный треугольник равнобедренный, то высота проведённая к основанию является ещё и медианой и делит основание на два равных прямоугольных треугольников. Рассмотрим один из них. Боковая сторона в полученном треугольнике является гипотенузой, а высота - катетом. Вычислим второй катет по теореме Пифагора:
25²- 15²=√(625-225)=√400=20
Этот катет равен половине основания данного треугольника, и поэтому его основание = 20×2=40см.
Основание= 40см
Теперь найдём площадь треугольника по формуле: ½×а×h, где h - его высота, "а"- сторона, к которой проведена высота:
S= ½ × 15×40= 300см²; S=300см²