Острый и тупой угол трапеции, прилежащие к одной и той же боковой стороне в сумме равны 180°. У нас равнобедренная трапеция. Это значит в ней два одинаковых острых и два одинаковых тупых угла, и поэтому неважно, противолежащие они или нет. Таким образом, зная разность и сумму острого и тупого углов (они жн противолежащие), легко вычислить углы. Обозначим любой из углов, например, тупой, как икс. А острый как игрек. Тогда Y=Х-40 или Y=180-Х, значит Х-40=180-Х; 2Х=180+40; Х=220:2=110°; Y=110-40=70° ответ: тупые углы равны 110°, а острые углы равны 70°
а) (-2;0) - центр окружности, радиус окружности равен 3.
б) (0; 4) - центр окружности, радиус окружности равен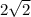 .
.
в) (5; -7) - центр окружности, радиус окружности равен 4.
Объяснение:
Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.
а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.
б) (0; 4) - центр окружности,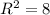 ,
, 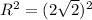
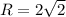 .
.
в) (5; -7) - центр окружности, R²=16,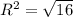 , R=4.
, R=4.
Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень
ответ: тупые углы равны 110°, а острые углы равны 70°