Отрежем от ромба его диагональю треугольник. Если ромб был АВСД, то берём треугольник АВС. Он равнобедренный, т.к. АВ=ВС. Значит отрезок, соединяющий середины сторон АВ и ВС является средней линией равнобедренного треугольника, а значит этот отрезок параллелен основанию АС. Аналогично повторяем рассуждения для треугольника AДС, и понимаем, что отрезок, соединяющий середины сторон АД и ДС есть средняя линия, значит он параллелен АС. Итак, имеем, что обе средние линии - треугольников АВС и АДС параллельны диагонали ромба АС, следовательно они параллельны друг другу.
Повторяем те же рассуждения для второй диагонали ромба - ВД, и так же получаем параллельность второй пары отрезков.
Следовательно, четырёхугольник, вершинами которого являются середины сторон ромба, является параллелограммом.
Далее, из симметрии ромба, замечаем, что обе диагонали этого получившегося четырёхугольника проходят через центр ромба, и равны между собой.
Параллелограмм, у которого диагонали равны - это и есть прямоугольник - что и требовалось доказать.
Ну, я бы так доказывал. Может кто-нибудь предложит более простой
№1: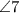 . №2:
. №2: 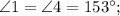
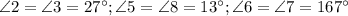 .
.
Объяснение:№1.
Пусть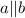 , тогда
, тогда  - секущая.
- секущая.
Теорема: "При пересечении двух параллельных прямых секущей, сумма односторонних углов равна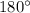 .
.
№2.
Обозначим данные прямые буквами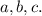
Пусть - секущая прямых
- секущая прямых  и
и 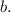
Теорема: "При пересечении двух параллельных прямых секущей, накрест лежащие углы равны".
============================================================
Свойство: "Вертикальные углы равны".
Свойство: "Сумма смежных углов равна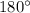 ".
".
Рассмотрим углы, образовавшиеся при пересечении прямых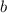 и
и 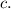
===========================================================
Рассмотрим углы, образовавшиеся при пересечении прямых и
и  .
.
Аналогично повторяем рассуждения для треугольника AДС, и понимаем, что отрезок, соединяющий середины сторон АД и ДС есть средняя линия, значит он параллелен АС.
Итак, имеем, что обе средние линии - треугольников АВС и АДС параллельны диагонали ромба АС, следовательно они параллельны друг другу.
Повторяем те же рассуждения для второй диагонали ромба - ВД, и так же получаем параллельность второй пары отрезков.
Следовательно, четырёхугольник, вершинами которого являются середины сторон ромба, является параллелограммом.
Далее, из симметрии ромба, замечаем, что обе диагонали этого получившегося четырёхугольника проходят через центр ромба, и равны между собой.
Параллелограмм, у которого диагонали равны - это и есть прямоугольник - что и требовалось доказать.
Ну, я бы так доказывал. Может кто-нибудь предложит более простой