1.Решить системы уравнений: а подстановки: 1) {+=75−7=11 ; 2) {−2=8 −3=6 ; 3) {+=65−2=9 ; б сложения: 1) {2−3=13+=7 ; 2) {2+5=−73−=15 ; 3) {−2=7 +2=−1 ; 4) {+3=7 +2=5 ; 2. Решить системы неравенств: а) {14+4>03+20<0 ; б) {−1≤2+23+5≤+1 ; в) {3−2≥+14−2≤−2; 3. Разложить на множители: а) b2 – c2 ; б) x2 – y2; в) a2 – 9 ; г) b2 – 16 ; д) x2 – 1; 4. Разложить на множители: а) 0,25a2 – 1; б) 0,16 – 4b2 ; в) 0,09x2 – y2 ; г)1,44a2 – 1,21; д) 14 a2 – 19 b2 ; 5. Вычислить: а) 372 – 132 ; б) 722 – 282 ; в) 42,42 – 42,32 ; г) 6,82 – 3,22 ; д) 19 ∙ 21 ; е) 99 ∙ 101;

1) Шаровой сегмент – это часть шара, ограниченная секущей плоскостью

2) Шаровой сектор — геометрическое тело, возникающее при вращении сектора вокруг одного из его радиусов или вокруг диаметра, не пересекающего его дуги

3) V конуса = ⅓πR²H

4) πR² * H =  ⅓πH (4^2 + 4 * 22 + 22^2)

   R =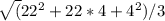 = 14 см

5) V = 4/3πR^3

50 : 2 = 25 см радиус 1 шара, объём V1 = 4/3π25^3.

70 : 2 = 35 см радиус 2 шара, объём V2 = 4/3π35^3.

Найти сумму объёмов V1 + V2 = 4/3π25^3 + 4/3π35^3 = 4/3π (25^3 + 35^3) = 4/3π (15 625 + 42 875) = 4/3π * 58 500 = V3

R = (V3 : 4/3π)1/3 = 58 5001/3 = 38,8

D = 2R = 38,8 * 2 = 77,6 см

6) r = 1/2 * d = 1/2 * 4 = 4/2 = 2 м.

L = √(h2 + r2) = √(3,52 + 22) = √12,25 + 4 = √16,25 = 4,03 м - длина основания

S =  π*R*L ; S = 3,14 * 2 * 4,03 = 6,28 * 4,0311 = 25,31 м^2

Мне кажется (мне может и не правильно казаться) правильно (да)

Пошаговое объяснение:

среднее арифметическое = 45:10=4. - в среднем получил каждый спортсмен.

Значит, если поделить всех спортсменов на (10:2) 5 пар, то сумма каждой пары будет равна (4.5*2)

9=1+8

9=2+7

9=3+6

9=4+5

и наоборот (5+4; 6+3; 7+2; 8+1)

Всего получается 5 пар, а кол-во вариантов разбалловок в каждой паре 4 (если не считать обратные). Следовательно как минимум у двух пар будут одинаковые разбалловки (значит в этих парах будут два спортсмена с одинаковым кол-во ), что и требовалось доказать.

P.s. моё решение может быть неправильным или некорректно оформленным.