Для бани нужно изготовить открытый чан, имеющий форму прямоугольного параллелепипеда, основанием которого является квадрат, сторона которого 2300 мм, а высота параллелепипеда 1500 . Для этого купили листы из нержавеющей стали размерами 1000 мм х 2000 мм. На швы и обрезки тратится 10% от площади всей поверхности. Вопрос 1: Чему равна площадь одного листа? ответ:
Вопрос 2: Чему равна площадь поверхности данного чана?
ответ:
Вопрос 3: Сколько уйдет материала с учетом швов и обрезков?
ответ:
Вопрос 4: Какое количество листов уйдет на изготовления чана?
ответ:
Вопрос 5: Сколько литров воды нужно, чтобы заполнить чан на 2/3?
ответ:
1) n = 2. Можно считать, что числа взаимно просты: если НОД равен d, то если разделить каждое из чисел на d, при этом сумма и НОК уменьшатся в d раз и равенство, если оно было, не нарушится.
Пусть числа равны a и b, тогда сумма a + b, НОК ab.
ab = a + b
ab - a - b + 1 = 1
(a - 1)(b - 1) = 1 — так не бывает при неравных натуральных a, b.
2) Пример для n = 3: числа 1, 2, 3. Сумма и НОК равны 6.
3) Если n > 3, подходят числа 1, 3, 2^2, 2^3, ..., 2^(n - 3), 3 * 2^(n - 2), 2^(n - 1). Сумма равна (1 + 2 + ... + 2^(n - 1)) + 1 + 2^(n - 1) = 2^n - 1 + 1 + 2^(n - 1) = 3 * 2^(n - 1), НОК равно 3 * 2^(n - 1).
Правильная четырехугольная пирамида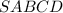 .
.
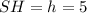 (см).
(см).
Найти: - сторону основания.
- сторону основания.
Решение:Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
Попробуем выразить через
через  (сторону основания) и
(сторону основания) и 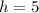 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный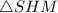 (где
(где 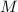 - середина
- середина 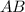 ). В нем
). В нем 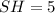 (см), а
(см), а 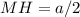 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что - неотрицательное):
- неотрицательное):
Пусть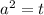 :
:
Второй корень нам не подходит по причине отрицательности. Значит:
Задача решена!
ответ: