Для некоторой функции f: x∈r→y∈r известно, что f(-10x-6)=70x+4. докажите что f(x) может быть представлена в виде f(x)=ax+b

Показать ответ

Ответ:

Dazzel09

29.09.2022 23:35

Для начала докажем то, что называется неравенством Коши-Буняковского-Шварца:

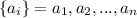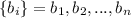Рассмотрим два набора чисел: $\{a_{i}\}=a_{1},a_{2},...,a_{n}$ и $\{b_{i}\}=b_{1},b_{2},...,b_{n}$ .

Тогда выполнено неравенство: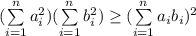 $(\sum\limits_{i=1}^{n}a_{i}^{2})(\sum\limits_{i=1}^{n}b_{i}^{2})\geq (\sum\limits_{i=1}^{n}a_{i}b_{i})^{2}$ ;

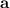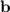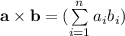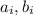Это неравенство можно доказывать по-разному. Заметим, что скалярное произведение векторов $\textbf{a}$ и $\textbf{b}$ есть $\textbf{a}\times\textbf{b}=(\sum\limits_{i=1}^{n}a_{i}b_{i})$ , где $a_{i},b_{i}$ - координаты составляющих вектора. Поскольку скалярное произведение векторов всегда не превосходит произведения модулей векторов (так как 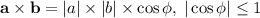$\textbf{a}\times\textbf{b}=|a|\times|b|\times\cos\phi,\; |\cos\phi|\leq 1$ ), то отсюда немедленно следует неравенство (ведь сумма квадратов в рассматриваемом неравенстве - это квадрат модуля вектора).

__________________________

Сделаем замену: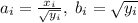 $a_{i}=\frac{x_{i}}{\sqrt{y_{i}}},\; b_{i}=\sqrt{y_{i}}$ ; Получим неравенство: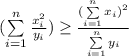 $(\sum\limits_{i=1}^{n}\frac{x_{i}^{2}}{y_{i}} )\geq \frac{(\sum\limits_{i=1}^{n}x_{i})^2}{\sum\limits_{i=1}^{n}y_{i}}$

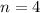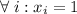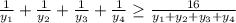
Полагая n=4 и $\forall\; i:x_{i}=1$ , получим: $\frac{1}{y_{1}}+\frac{1}{y_{2}}+\frac{1}{y_{3}}+\frac{1}{y_{4}}\geq \frac{16}{y_{1}+y_{2}+y_{3}+y_{4}}$

0,0(0 оценок)

Ответ:

0123220210

19.01.2022 16:22

Объектом изучения теории вероятностей являются события и их вероятности. Если событие является сложным, то его можно разбить на простые составляющие, вероятности которых найти несложно.

Суммой событий А и В называется событие С, заключающееся в том, что произошло либо событие А, либо событие В, либо события А и В одновременно.

Произведением событий А и В называется событие С, заключающееся в том, что произошло и событие А и событие В.

IСобытия А и В называется несовместными, если они не могут произойти одновременно.

Событие А называется невозможным, если оно не может произойти. Такое событие обозначается символом \oslash.

Событие А называется достоверным, если оно обязательно произойдет. Такое событие обозначается символом \Omega.I

Пусть каждому событию А поставлено в соответствие число P{А). Это число P(А) называется вероятностью события А, если при таком соответствии выполнены следующие условия.

1.Вероятность принимает значения на отрезке от 0 до 1, т.е. 0<P(A)<1

2.Вероятность невозможного события равна 0, т.е. P(\oslash) = 0 .

3.bВероятность достоверного события равна 1, т.e. P(\Omega) = 1.

4.Если события A и В несовместные, то вероятность их суммы равна сумме их вероятностей, т.е. P(A+B) =P(A)+P(B)

Важным частным случаем является ситуация, когда имеется n равновероятных элементарных исходов, и произвольные k из этих исходов образуют события А. В этом случае вероятность можно ввести по формуле P(A) = \frac{k}{n}. Вероятность, введенная таким образом, называется классической вероятностью. Можно доказать, что в этом случае свойства 1-4 выполнены.

Задачи по теории вероятностей, которые встречаются на ЕГЭ по математике, в основном связаны с классической вероятностью. Такие задачи могут быть очень простыми. Особенно простыми являются задачи по теории вероятностей в демонстрационных вариантах. Легко вычислить число благоприятных исходов k, прямо в условии написано число всех исходов n.

0,0(0 оценок)

Популярные вопросы: Математика