Известны координаты А(-2;-3), B(1;6), C(6;1) в прямоугольной системе координат Oxy трех точек A,B,C, являющихся вершинами треугольника. Изобразить треугольник ABC в этой прямоугольной системе координат и найти: 3.1 координаты векторов AB, AC и их длины;
3.2 скалярное произведение векторов AB, AC и угол ф между векторами AB, AC ;
3.3 векторное произведение векторов , и площадь треугольника ;
3.4 значение параметра β , при котором векторы АВ + β * АС и ВС будут коллинеарны;
3.5 координаты точки Р , делящей отрезок АВ в отношении Ʌ =1/2 ;
3.6 каноническое уравнение стороны АВ ;
3.7 уравнение с угловым коэффициентом и угловой коэффициент прямой, проходящей через точку параллельно прямой АВ;

Единичный отрезок разбит на 3 части, значит в одном маленьком делении содержится 1/3 единицы измерения (цена деления = 1/3 ) .

Точка Е находится на расстоянии 1/3 от 0 вправо ( в положительном направлении) . Значит координата точки Е - это 1/3 , обозначаем так  Е(1/3) .

Точка A находится на расстоянии 1/3 от 0 влево ( в отрицательном направлении) . Значит координата точки А - это  -1/3 , обозначаем так  А(-1/3) .

Точка F находится на расстоянии 2/3 от  1  вправо ( в положительном направлении) . Значит координата точки F - это 1 +2/3=1 целая и 2/3 , обозначаем так   .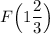

Аналогично, определяем    .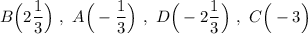

Пусть х - скорость одного туриста

(х+1,5) - скорость другого

За 4 1/4 часа первый пройдет х*4 1/4 км

                                     второй  (х+1,5)*4 1/4 км

вместе они пройдут 34 км; составим уравнение

4 1/4*х + 4 1/4*(х+1,5)=34 вынесем 4 1/4 за скобки

4 1/4 (х+х+1,5)=34  переведем 4 1/4 в неправильную дробь

17/4 * (2х+1,5)=34  разделим обе части уравнения на 17

1/4 * (2х+1,5)=2   умножим обе части на 4

2х+1,5=8

2х=8-1,5

2х=6,5

х=3,25 км/ч - скорость одного туриста

3,25+1,5=4,75 км/ч - скорость второго. Это ответ.