Мен көптеген туыстары, әкем және анамның тарапымен де бар. Менің анам мен әкем өзбектер. Менің анам, екі iнiлерi мен апа. Оның екінші ағасы автомобиль апатында қаза тапты. ағасы үш ұлдары, орташа шешесінің ағасы, екі қызы және ұлы, тым әпкесі, оның үш ұлы, ал анам екі қызы және ұлы бар. Анам, сондай-ақ бауырларын бар. Менің ана бір немере бес және жеті апалы-сіңлілі Әкем бір ғана қарындасы. Ол ұлы және қызы бар. Ол төрт ағасы және екі әпкесімен отбасы бар күйеуі бар. Олар сондай-ақ менің туыстарым қарастырылады. Менің отбасым інілері мен әпкелері бастап. Сіңлім үйленді, ол қазірдің өзінде бір қызы бар. Менің барлық туыстары жақсы көремін!
1) Область определения функции
2) Точки пересечения графика функции с осью OY
3) Исследуем функции на четность
Так как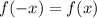
, то функция является четной
4) Функция имеет две точки разрыва -1 и 1 , поэтому график функции имеет две вертикальные асимптоты х =-1 и х =1.
Найдем наклонные асимптоты
, где
Так как k=0, то наклонных асимптот нет, а есть горизонтальные.
Найдем теперь коэффициент b.
Подставляем найденные коэффициенты в формулу y = kx + b, получаем, что y = 0 - горизонтальная асимптота.
5) Найдем экстремумы функции. Для это найдем производную y' и приравняем ее к нулю y' = 0
Тогда
Получилась одна критическая точка.
6) Найденные точки разрыва и точки экстремума, разбивают область определения на четыре интервала. Находим знак производной (у') на каждом интервале.
x x<-1 -1<x<0 0 0<x<1 x>1
y' - - 0 + +
y убыв. убыв. 1 воз. воз.
В точке экстремума (х=0) производная меняет знак с "-" на "+" значит это точка минимума.
7) Найдем точки перегиба и промежутки выпуклости и вогнутости. Для этого найдем вторую производную
Решаем методом интервалов
Корней нет, значит точек перегиба нет и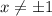
Отмечаем на числовой прямой все найденные точки разрыва и критические точки , в нашем случае это точки –1; 0 ; 1.
Методом интервалов определяем знаки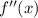
на полученных интервалах.
Интервал X < -1 ,
f''(x) = "–" < 0 - график функции является выпуклым на данном интервале;
Интервал – 1 < X < 1 ,
f''(x) = "+" > 0 - график функции является вогнутым на данном интервале;
Интервал X > 1 ,
f''(x) = "–" < 0 - график функции является выпуклым на данном интервале;
8) Построим график функции. Данные для построения и сам график, представлены ниже