Если для любого из области определения функции выполняется равенство , то функция является чётной.
Если для любого из области определения функции выполняется равенство , то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда .
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём , для этого все в функции заменим на .
Таким образом, данная функция является нечётной.
в)
То есть, для данной функции за можно принять любое действительное число. Теперь найдём , для этого все в функции заменим на .
Таким образом, данная функция является чётной.
г)
может быть любым числом, поскольку никаких ограничений на аргумент здесь не накладывается. Теперь найдём , для этого все в функции заменим на .
.
и , а значит, функция не является ни чётной, ни нечётной.
В решении.
Пошаговое объяснение:
1) 1 и 2/3 - b = 5/6
-b = 5/6 - 1 и 2/3
b = 1 и 2/3 - 5/6
b = 5/6.
2) х : 0,2 = 1 и 1/3
х = 0,2 * 1 и 1/3
х = 1/5 * 4/3
х = 4/15.
3) 7/12 + а = 1 и 1/6
а = 1 и 1/6 - 7/12
а = 7/6 - 7/12
а = 14/12 - 7/12
а = 7/12.
4) у * 2/7 = 3/14
у = 3/14 : 2/7
у = (3 * 7)/(14 * 2)
у = 3/4.
5) 6/7 : с = 3/14
с = 6/7 : 3/14
с = (6 * 14)/(7 * 3)
с = 4.
6) с + 1 и 1/3 = 3
с = 3 - 1 и 1/3
с = 1 и 2/3.
7) а : 2/3 = 3/4
а = 3/4 * 2/3
а = (3 * 2)/(4 * 3)
а = 1/2.
8) у - 5/6 = 1/3
у = 1/3 + 5/6
у = 2/6 + 5/6
у = 7/6.
9) 1 и 5/6 - у = 2/3
-у = 2/3 - 1 и 5/6
у = 1 и 5/6 - 2/3
у = 1 и 5/6 - 4/6
у = 1 и 1/6.
10) х - 7/10 = 7/10
х - 0,7 = 0,7
х = 0,7 + 0,7
х = 1,4.
Проверка путём подстановки вычисленных значений неизвестных в уравнения показала, что данные решения удовлетворяют данным уравнениям.
Если для любого
из области определения функции выполняется равенство 
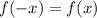, то функция является чётной.
Если для любого
из области определения функции выполняется равенство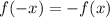 
, то данная функция является нечётной.
Если же ни одно из этих равенств не выполняется, то функция не является ни чётной, ни нечётной.
б)
Отсюда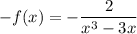
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
Итак, область определения нашли. Теперь найдём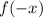
, для этого все 
в функции заменим на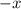 
.
Таким образом, данная функция является нечётной.
в)
Отсюда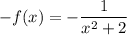
.
Для начала найдём область определения данной функции. Её знаменатель не должен быть равен нулю:
То есть, для данной функции за
можно принять любое действительное число. Теперь найдём 
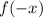, для этого все 
в функции заменим на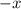 
.
Таким образом, данная функция является чётной.
г)
Отсюда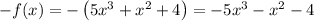
.
В решении.
Пошаговое объяснение:
1) 1 и 2/3 - b = 5/6
-b = 5/6 - 1 и 2/3
b = 1 и 2/3 - 5/6
b = 5/6.
2) х : 0,2 = 1 и 1/3
х = 0,2 * 1 и 1/3
х = 1/5 * 4/3
х = 4/15.
3) 7/12 + а = 1 и 1/6
а = 1 и 1/6 - 7/12
а = 7/6 - 7/12
а = 14/12 - 7/12
а = 7/12.
4) у * 2/7 = 3/14
у = 3/14 : 2/7
у = (3 * 7)/(14 * 2)
у = 3/4.
5) 6/7 : с = 3/14
с = 6/7 : 3/14
с = (6 * 14)/(7 * 3)
с = 4.
6) с + 1 и 1/3 = 3
с = 3 - 1 и 1/3
с = 1 и 2/3.
7) а : 2/3 = 3/4
а = 3/4 * 2/3
а = (3 * 2)/(4 * 3)
а = 1/2.
8) у - 5/6 = 1/3
у = 1/3 + 5/6
у = 2/6 + 5/6
у = 7/6.
9) 1 и 5/6 - у = 2/3
-у = 2/3 - 1 и 5/6
у = 1 и 5/6 - 2/3
у = 1 и 5/6 - 4/6
у = 1 и 1/6.
10) х - 7/10 = 7/10
х - 0,7 = 0,7
х = 0,7 + 0,7
х = 1,4.
Проверка путём подстановки вычисленных значений неизвестных в уравнения показала, что данные решения удовлетворяют данным уравнениям.