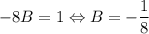Математика: Найти интегралы методом подстановки

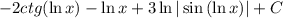
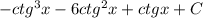
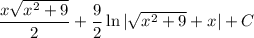
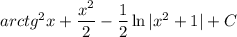
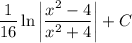
1) 2) 3) 4) 5) Пошаговое объяснение:1)2)3)Первый интеграл проинтегрируем по частям:Найдём неизвестный интеграл следующим образом:Неизвестные коэффициенты найдём методом частных значений:При y = 1: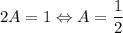 При y = -1: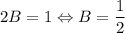 4)5)Разложим дробь на простейшие:Найдём коэффициенты методом частных значений:При y = 4: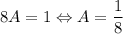 При y = -4:...

Найти интегралы методом подстановки

Показать ответ

Ответ:

kris0287

07.03.2022 06:00

1) $-2ctg(\ln{x})-\ln{x}+3\ln{|\sin{(\ln{x})}|}+C$

2) -ctg^3x-6ctg^2x+ctgx+C

3) $\dfrac{x\sqrt{x^2+9}}{2}+\dfrac{9}{2}\ln{|\sqrt{x^2+9}+x}|}+C$

4) $arctg^2x+\dfrac{x^2}{2}-\dfrac{1}{2}\ln{|x^2+1|}+C$

5) $\dfrac{1}{16}\ln{\left|\dfrac{x^2-4}{x^2+4}\right|}+C$

Пошаговое объяснение:

$\displaystyle \int\dfrac{2ctg^2(\ln{x})+3ctg(\ln{x})+1}{x}dx=\int (2ctg^2(\ln{x})+3ctg(\ln{x})+1)d(\ln{x})=\\=2\int \left(\dfrac{1}{\sin^2{(\ln{x})}}-1\right)d(\ln{x})+3\int \dfrac{\cos{(\ln{x})}d(\ln{x})}{\sin{(\ln{x})}}+\int d(\ln{x})=\\=-2ctg(\ln{x})-2\ln{x}+3\int \dfrac{d(\sin{(\ln{x})})}{\sin{(\ln{x})}}+\ln{x}+C=\\=-2ctg(\ln{x})-\ln{x}+3\ln{|\sin{(\ln{x})}|}+C$

$\displaystyle \int \dfrac{3ctg^2x+12ctgx-1}{\sin^2{x}}dx=-\int (3ctg^2x+12ctgx-1)d(ctgx)=\\=-ctg^3x-6ctg^2x+ctgx+C$

$\displaystyle \int\sqrt{x^2+9}dx=\left[x=3tgt,dx=\dfrac{3dt}{\cos^2{t}},t=arctg\dfrac{x}{3}\right]=\int \dfrac{3\sqrt{9tg^2t+9}dt}{\cos^2{t}}=\\=\int \dfrac{9\sqrt{tg^2t+1}dt}{\cos^2{t}}=9\int\dfrac{\sqrt{\frac{1}{\cos^2{t{\cos^2{t}}dt=9\int \dfrac{dt}{\cos^3{t}}=9\int\dfrac{\sin^2{t}+\cos^2{t}}{\cos^3{t}}dt=\\=9\int \dfrac{\sin^2{t}dt}{\cos^3{t}}+9\int \dfrac{dt}{\cos{t}}=(*)$

Первый интеграл проинтегрируем по частям:

$\displaystyle \int\dfrac{\sin^2{t}dt}{\cos^3{t}}=\left[u=\sin{t},dv=\dfrac{\sin{t}dt}{\cos^3{t}}\Rightarrow du=\cos{t}dt,v=\dfrac{1}{2\cos^2{t}}\right]=\\=\dfrac{\sin{t}}{2\cos^2{t}}-\dfrac{1}{2}\int\dfrac{dt}{\cos{t}}$

$\displaystyle (*)=\dfrac{9\sin{t}}{2\cos^2{t}}-\dfrac{9}{2}\int\dfrac{dt}{\cos{t}}+9\int\dfrac{dt}{\cos{t}}=\dfrac{9\sin{t}}{2\cos^2{t}}+\dfrac{9}{2}\int\dfrac{dt}{\cos{t}}=(**)$

Найдём неизвестный интеграл следующим образом:

$\displaystyle \int\dfrac{dt}{\cos{t}}=\int\dfrac{\cos{t}dt}{\cos^2{t}}=\int\dfrac{d(\sin{t})}{1-\sin^2{t}}\\\dfrac{1}{1-y^2}=\dfrac{A}{1-y}+\dfrac{B}{1+y}=\dfrac{A(1+y)+B(1-y)}{1-y^2}$

Неизвестные коэффициенты найдём методом частных значений:

При y = 1: $2A=1\Leftrightarrow A=\dfrac{1}{2}$

При y = -1: $2B=1\Leftrightarrow B=\dfrac{1}{2}$

$\displaystyle \dfrac{1}{1-y^2}=\dfrac{1}{2(1-y)}+\dfrac{1}{2(1+y)}\\\int\dfrac{d(\sin{t})}{1-\sin^2{t}}=\int\left(\dfrac{1}{2(1-\sin{t})}+\dfrac{1}{2(1+\sin{t})}\right)d(\sin{t})=\dfrac{1}{2}\int\dfrac{d(\sin{t})}{1-\sin{t}}+\\+\dfrac{1}{2}\int\dfrac{d(\sin{t})}{1+\sin{t}}=-\dfrac{1}{2}\ln{|1-\sin{t}|}+\dfrac{1}{2}\ln{|1+\sin{t}|}+C=\dfrac{1}{2}\ln{\left|\dfrac{1+\sin{t}}{1-\sin{t}}\right|}+C=\\=\dfrac{1}{2}\ln{\left|\dfrac{(1+\sin{t})^2}{(1-\sin{t})(1+\sin{t})}\right|}+C=$

$=\dfrac{1}{2}\ln{\left|\dfrac{(1+\sin{t})^2}{1-\sin^2{t}}\right|}+C=\dfrac{1}{2}\ln{\left|\dfrac{(1+\sin{t})^2}{\cos^2{t}}\right|}+C=\dfrac{1}{2}\ln{\left(\dfrac{1+\sin{t}}{\cos{t}}\right)^2}+C=\\=\ln{\left|\dfrac{1}{\cos{t}}+tgt\right|}+C$

$\displaystyle (**)=\dfrac{9tgt}{2\cos{t}}+\dfrac{9}{2}\ln{\left|\dfrac{1}{\cos{t}}+tgt\right|}+C=\dfrac{9tg(arctg\frac{x}{3})}{2\cos{(arctg\frac{x}{3})}}+\\+\dfrac{9}{2}\ln{\left|\dfrac{1}{\cos{(arctg\frac{x}{3})}}+tg\left(arctg\frac{x}{3}\right)\right|}+C=\dfrac{3x}{\frac{2}{\sqrt{1+\frac{x^2}{9+\dfrac{9}{2}\ln{\left|\dfrac{1}{\frac{1}{\sqrt{1+\frac{x^2}{9+\dfrac{x}{3}\right|}+C=\\=\dfrac{3x\sqrt{1+\frac{x^2}{9}}}{2}+\dfrac{9}{2}\ln{\left|\dfrac{3\sqrt{1+\frac{x^2}{9}}+x}{3}\right|}+C=$

$=\dfrac{x\sqrt{x^2+9}}{2}+\dfrac{9}{2}\ln{\left|\dfrac{\sqrt{x^2+9}+x}{3}\right|}+C=\dfrac{x\sqrt{x^2+9}}{2}+\dfrac{9}{2}\ln{|\sqrt{x^2+9}+x}|}-\\-\dfrac{9}{2}\ln{3}+C=\dfrac{x\sqrt{x^2+9}}{2}+\dfrac{9}{2}\ln{|\sqrt{x^2+9}+x}|}+C$

$\displaystyle \int\dfrac{2arctgx+x^3}{1+x^2}dx=\int\dfrac{2arctgx}{1+x^2}dx+\int\dfrac{x^3}{1+x^2}dx=\int 2arctgxd(arctgx)+\\+\int\left(x-\dfrac{x}{x^2+1}\right)dx=arctg^2x+\dfrac{x^2}{2}-\int\dfrac{xdx}{x^2+1}+C=arctg^2x+\dfrac{x^2}{2}-\\-\dfrac{1}{2}\int \dfrac{d(x^2+1)}{x^2+1}+C=arctg^2x+\dfrac{x^2}{2}-\dfrac{1}{2}\ln{|x^2+1|}+C$

$\displaystyle \int\dfrac{xdx}{x^4-16}=\dfrac{1}{2}\int\dfrac{d(x^2)}{(x^2-4)(x^2+4)}=(*)$

Разложим дробь на простейшие:

$\dfrac{1}{y^2-16}=\dfrac{A}{y-4}+\dfrac{B}{y+4}=\dfrac{A(y+4)+B(y-4)}{y^2-16}$

Найдём коэффициенты методом частных значений:

При y = 4: $8A=1\Leftrightarrow A=\dfrac{1}{8}$

При y = -4: $-8B=1\Leftrightarrow B=-\dfrac{1}{8}$

$\displaystyle \dfrac{1}{y^2-16}=\dfrac{1}{8(y-4)}-\dfrac{1}{8(y+4)}\\(*)=\dfrac{1}{2}\left(\dfrac{1}{8}\int\dfrac{d(x^2)}{x^2-4}-\dfrac{1}{8}\int\dfrac{d(x^2)}{x^2+4}\right)=\dfrac{1}{16}(\ln{|x^2-4|}-\ln{|x^2+4|})+C=\\=\dfrac{1}{16}\ln{\left|\dfrac{x^2-4}{x^2+4}\right|}+C$