Перевод: Поезд проехал первую половину расстояния между двумя городами со скоростью 72,75 км/ч за 2,4 часа, а вторую половину за 3,6 часа. Найдите среднюю скорость поезда.
Решение. Пройдённый путь S зависит от скорости υ и времени t через формулу: S = υ • t.
Если объект проехал расстояние S1 за время t1, а расстояние S2 за время t2, то средняя скорость объекта равна:
υ = (S1 + S2)/( t1 + t2).
Так как υ1 = 72,75 км/ч и t1 = 2,4 ч, то половина расстояния между двумя городами равна
S1 = υ1 • t1 = 72,75 км/ч • 2,4 ч = 174,6 км.
Вторая половина пути равна к первой, то есть S2 = S1 = 174,6 км и t2 = 3,6 ч. Находим среднюю скорость движения поезда
υ = (S1 + S2)/( t1 + t2) = (174,6 км + 174,6 км) /(2,4 ч +3,6 ч) =
= 349,2 км/6 ч = 58,2 км/ч.
По автора задачи (машинный) перевод на казахский:
Шешімі. Жүрген қашықтық S жылдамдығы t жылдамдығына және формула бойынша t уақытқа байланысты: S = υ • t.
Егер объект S1 қашықтықты t1 уақытында, ал S2 қашықтық t2 уақытында өткен болса, онда объектінің орташа жылдамдығы:
υ = (S1 + S2) / (t1 + t2).
υ1 = 72,75 км / сағ және t1 = 2,4 сағат болғандықтан, екі қала арасындағы арақашықтықтың жартысы
S1 = υ1 • t1 = 72,75 км / сағ • 2,4 с = 174,6 км.
Жолдың екінші жартысы біріншіге тең, яғни S2 = S1 = 174.6 км және t2 = 3,6 сағат.
υ = (S1 + S2) / (t1 + t2) = (174,6 км + 174,6 км) / (2,4 сағат +3,6 сағат) =
58,2 км/ч или 58,2 км/сағ
Пошаговое объяснение:
Перевод: Поезд проехал первую половину расстояния между двумя городами со скоростью 72,75 км/ч за 2,4 часа, а вторую половину за 3,6 часа. Найдите среднюю скорость поезда.
Решение. Пройдённый путь S зависит от скорости υ и времени t через формулу: S = υ • t.
Если объект проехал расстояние S1 за время t1, а расстояние S2 за время t2, то средняя скорость объекта равна:
υ = (S1 + S2)/( t1 + t2).
Так как υ1 = 72,75 км/ч и t1 = 2,4 ч, то половина расстояния между двумя городами равна
S1 = υ1 • t1 = 72,75 км/ч • 2,4 ч = 174,6 км.
Вторая половина пути равна к первой, то есть S2 = S1 = 174,6 км и t2 = 3,6 ч. Находим среднюю скорость движения поезда
υ = (S1 + S2)/( t1 + t2) = (174,6 км + 174,6 км) /(2,4 ч +3,6 ч) =
= 349,2 км/6 ч = 58,2 км/ч.
По автора задачи (машинный) перевод на казахский:
Шешімі. Жүрген қашықтық S жылдамдығы t жылдамдығына және формула бойынша t уақытқа байланысты: S = υ • t.
Егер объект S1 қашықтықты t1 уақытында, ал S2 қашықтық t2 уақытында өткен болса, онда объектінің орташа жылдамдығы:
υ = (S1 + S2) / (t1 + t2).
υ1 = 72,75 км / сағ және t1 = 2,4 сағат болғандықтан, екі қала арасындағы арақашықтықтың жартысы
S1 = υ1 • t1 = 72,75 км / сағ • 2,4 с = 174,6 км.
Жолдың екінші жартысы біріншіге тең, яғни S2 = S1 = 174.6 км және t2 = 3,6 сағат.
υ = (S1 + S2) / (t1 + t2) = (174,6 км + 174,6 км) / (2,4 сағат +3,6 сағат) =
= 349,2 км/6 сағ = 58,2 км/сағ.
1. Чтобы найти радиус описанной около трапеции окружности, заметим, что эта окружность описана ещё и около треугольника ABC, из теоремы синусов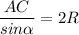
Надо найти AC.
Это можно сделать через теорему косинусов в треугольнике ABC.
Но для этого надо знать AB=a (боковая сторона трапеции) и BC=b (меньшее основание)
Нам же известен угол и радиус вписанной окружности.
Известный факт, что в трапецию если можно вписать окружность, то сумма противоположных сторон равна.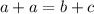 (c- большее основание).
(c- большее основание).
Далее из треугольника CHD ∠CDH=180-α;
Далее имеем систему с неизвестными b и c:
Из 2-го уравнения имеем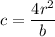
Подставляем в 1-е и получаем:
Это квадратное уравнение относительно b:
Все величины положительны, поэтому модули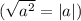 раскрываются с "+".
раскрываются с "+".
Не понятно пока, оставлять ли оба значения или брать одно, Попробуем вычислить с:
Надо учесть, что b<c. Всё будет зависеть от знаков, которые мы берем.
Чтобы с было больше b, с "+",
с "+", 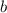 с "-".
с "-".
Но нам толком и не надо. Только
толком и не надо. Только 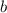
Теперь запишем теорему косинусов (AC=d):
Вспоминаем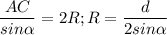
Дальше я не вижу смысла преобразовывать тригонометрию, там вроде ничего путного не выходит.
ответ: