Решение. Убедимся, что точка не лежит на прямой, данной в условии:
4/5 ≠ (3-1)/-1 ≠ (1+3)/3.
Из уравнения данной прямой следует, что точка M1(0;1; -3) лежит на этой прямой.
Пусть M(x;y;z) - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4) и s(5; -1; 3) компланарны. Следовательно, их смешанное произведение равно нулю:
Дано: Треугольник АВС — равнобедренный Р треугольника АВС = 30 см АС = 12 см ______________ Найти: ВК — ?
Решение:
Первое действие :
Периметр — сумма всех сторон ( Р=а+b+c) АВ=ВС ( по свойствам равнобедренных треугольников) Пусть АВ=ВС=х, составим уравнение: 12+х+х=30 см 12+2х=30 2х=30-12 2х=18 х=9 АВ=ВС=9 см ______ Второе действие:
ВК — высота, но также и медиана, и биссектриса(по свойству равнобедренных треугольников), поэтому 12:2=6=АК=КС Высота ВК создаёт прямой угол в 90 градусов ( угол АКВ и СКВ), поэтому треугольники АВК и СВК - прямоугольные треугольники. Рассмотрим треугольник АВК: АВ=9 см АК= 6 см Угол АКВ = 90 градусов Треугольник прямоугольный и имеются две стороны. Из этого следует, что мы можем воспользоваться теоремой Пифагора (а во второй степени(катет)+ b во второй степени(катет) = с во второй степени( гипотенуза)), чтобы узнать третью сторону, ВК. 9 во второй степени - 6 во второй степени = ВК во второй степени 81 - 36 = 45 ВК = корень из 45 = 2 корня из 10
Провести плоскость через прямую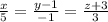
и точку Mo(4; 3; 1).
Решение. Убедимся, что точка не лежит на прямой, данной в условии:
4/5 ≠ (3-1)/-1 ≠ (1+3)/3.
Из уравнения данной прямой следует, что точка M1(0;1; -3) лежит на этой прямой.
Пусть M(x;y;z) - произвольная точка искомой плоскости, тогда векторы MoM(x-4; y-3; z-1), M1Mo(4; 2; 4) и s(5; -1; 3) компланарны. Следовательно, их смешанное произведение равно нулю:
x-4 y-3 z-1| x-4 y-3
4 2 4| 4 2
5 -1 3| 5 -1 =
= 6(x-4) + 20(y-3) - 4(z-1) - 12(y-3) + 4(x-4) - 10(z-1) =
= 6x -24 +20y - 60 - 4z + 4 - 12y + 36 + 4x - 16 - 10z + 10 =
= 10x + 8y - 14z - 50 = 0 или, сократив на 2:
5x + 4y - 7z - 25 = 0.
Таким образом, нормальный вектор искомой плоскости равен:
(5; 4; -7).
_______________
Дано:
Треугольник АВС — равнобедренный
Р треугольника АВС = 30 см
АС = 12 см
______________
Найти: ВК — ?
Решение:
Первое действие :
Периметр — сумма всех сторон ( Р=а+b+c)
АВ=ВС ( по свойствам равнобедренных треугольников)
Пусть АВ=ВС=х, составим уравнение:
12+х+х=30 см
12+2х=30
2х=30-12
2х=18
х=9
АВ=ВС=9 см
______
Второе действие:
ВК — высота, но также и медиана, и биссектриса(по свойству равнобедренных треугольников), поэтому 12:2=6=АК=КС
Высота ВК создаёт прямой угол в 90 градусов ( угол АКВ и СКВ), поэтому треугольники АВК и СВК - прямоугольные треугольники.
Рассмотрим треугольник АВК:
АВ=9 см
АК= 6 см
Угол АКВ = 90 градусов
Треугольник прямоугольный и имеются две стороны.
Из этого следует, что мы можем воспользоваться теоремой Пифагора (а во второй степени(катет)+ b во второй степени(катет) = с во второй степени( гипотенуза)), чтобы узнать третью сторону, ВК.
9 во второй степени - 6 во второй степени = ВК во второй степени
81 - 36 = 45
ВК = корень из 45 = 2 корня из 10
ответ: ВК = 2 корня из 10
Остальные решаются на подобии.
Надеюсь