(где V-объём правильной шестиугольной пирамиды, So.- площадь основания пирамиды, h- высота пирамиды).
"Как видите, ни один из элементов формулы нам пока не известен. Нужно выразить их из данных условия, т.е. через площадь боковой поверхности пирамиды."
(где Sb.- площадь боковой поверхности шестиугольной правильной пирамиды, P- периметр основания, a- апофема пирамиды.)
Так как основанием пирамиды является правильный шестиугольник, то
(где b-длина стороны основания)
Учитывая, что угол между боковой гранью и основанием равен 30°, то апофема и высота пирамиды относятся, как, соответственно, гипотенуза и меньший катет в прямоугольном треугольнике, т.е.
; (из прямоугольного треугольника, образованного апофемой, высотой пирамиды и проекцией апофемы на основание h=a*sin(30°))
Найдём отношение площади боковой поверхности Sb. и площади основания Sо. Каждая из поверхностей раскладывается на 6 равных треугольников.
Площадь бокового треугольника равна
Площадь треугольника основания равна
(т.к. высота в таком треугольнике есть проекцией апофемы на основание и равна
a*cos(30°)=).
Значит отношение площади боковой поверхности и площади основания равно:
Тогда площадь основания So можно выразить через площадь боковой поверхности как:
Теперь, чтобы найти высоту пирамиды, нужно выразить апофему а через площадь боковой поверхности Sb.
Основание - правильный шестиугольник, состоит из 6 правильных треугольников с внутренними углами по 60°. Высоту такого треугольника мы уже находили . Такая высота (являясь также биссектрисой) делит правильный треугольник на 2 прямоугольных с прилежащим к ней углом 30° (60°/2=30°).
Тогда сторона b правильного треугольника равна
b=a.
Подставив полученные выражения в формулу боковой поверхности, получим:
⇔
а так, как мы вывели, что , то
Теперь все неизвестные выражены через площадь боковой поверхности и мы можем вычислить объём пирамиды:
*в решении задачи многократно применялась теорема Пифагора. Чтобы сократить текст решения, я это опустил.
Переводим в меньшие единицы- умножаем;(3кг 20г= 3•1000г+20г= 3000г+20г=3020г ) ; переводим в большие - делим с остатком; пишем целые в больших и остаток остаётся в меньших единицах ( 130см: 100=1м ост 30см)
Пошаговое объяснение:
"Как видите, ни один из элементов формулы нам пока не известен. Нужно выразить их из данных условия, т.е. через площадь боковой поверхности пирамиды."
Так как основанием пирамиды является правильный шестиугольник, то
Учитывая, что угол между боковой гранью и основанием равен 30°, то апофема и высота пирамиды относятся, как, соответственно, гипотенуза и меньший катет в прямоугольном треугольнике, т.е.
Найдём отношение площади боковой поверхности Sb. и площади основания Sо. Каждая из поверхностей раскладывается на 6 равных треугольников.
Площадь бокового треугольника равна
Площадь треугольника основания равна
a*cos(30°)=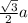 ).
).
Значит отношение площади боковой поверхности и площади основания равно:
Тогда площадь основания So можно выразить через площадь боковой поверхности как:
Теперь, чтобы найти высоту пирамиды, нужно выразить апофему а через площадь боковой поверхности Sb.
Основание - правильный шестиугольник, состоит из 6 правильных треугольников с внутренними углами по 60°. Высоту такого треугольника мы уже находили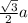 . Такая высота (являясь также биссектрисой) делит правильный треугольник на 2 прямоугольных с прилежащим к ней углом 30° (60°/2=30°).
. Такая высота (являясь также биссектрисой) делит правильный треугольник на 2 прямоугольных с прилежащим к ней углом 30° (60°/2=30°).
Тогда сторона b правильного треугольника равна
b=a.
Подставив полученные выражения в формулу боковой поверхности, получим:
а так, как мы вывели, что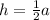 , то
, то
Теперь все неизвестные выражены через площадь боковой поверхности и мы можем вычислить объём пирамиды:
*в решении задачи многократно применялась теорема Пифагора. Чтобы сократить текст решения, я это опустил.
3м 78см * 5 = (3•100см+ 78 см) • 5= 378см • 5= 1890см= (1890см:100)=
18м 90 см
1кг=1000 г
17кг 675г * 24 =( 17•1000г+675г) • 24=
17675г• 24= 424200г = (424200г:1000)= 424кг 200г
1час= 60 минут
4ч 27мин * 19= (4•60мин+ 27мин )•19 =
267мин • 19= 5073мин= (5073мин:60)= 84ч 33 мин
Второй
3м 78см * 5= 3м• 5+ 78см• 5=
15м+ 390см= 15м+ (390см:100)= 15м+ 3м 90см= 18м 90 см
17кг 675г * 24= 17кг•24+ 675г•24=
408кг+ 16200г= 408кг+ (16200г:1000)=
408кг+ 16кг 200г= 424 кг 200 г
4ч 27мин * 19 = 4ч• 19+ 27мин• 19=
76ч + 513 мин= 76ч+ (513мин : 60)=
76ч+ 8ч 33мин= 84ч 33 мин
Переводим в меньшие единицы- умножаем;(3кг 20г= 3•1000г+20г= 3000г+20г=3020г ) ; переводим в большие - делим с остатком; пишем целые в больших и остаток остаётся в меньших единицах ( 130см: 100=1м ост 30см)