В коробке лежат чёрные, белые и красные шарики. Чёрных больше, чем 7, а белых меньше, чем 7. Вместе чёрных и красных в 2 раза больше, чем белых, а белых и красных ровно столько, сколько чёрных. Сколько всего шариков?
РЕШЕНИЕ: Пусть черных с, белых b, красных k.
Складываем уравнения:
Подставляем во второе:
Единственное возможное целое k - число 3.
Тогда k+c+b=k+3k+2k=6k=6*3=18 шариков
ОТВЕТ: 18 шариков
Задание № 5:
Стоя неподвижно на ступени эскалатора в метро Ваня поднимается наверх за одну минуту. Взбегая по ступеням неподвижного эскалатора, он добирается до верха за 40 секунд. За какое время Ваня поднимается наверх, если начинает взбегать по ступеням эскалатора, движущегося вверх? Дайте ответ в секундах.
РЕШЕНИЕ: Пусть длина расстояния L.
Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60. (Считаем в секундах, в минуте 60 секунд).
Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40.
Когда Ваня бежит по ступеням движущегося эскалатора, то скорости Вани и эскалатора суммируются: L/60+L/40. Тогда время определяется отношением длины к скорости:
ОТВЕТ: 24 секунды
Задание № 6:
Встретились три охотника и сварили кашу. Первый дал две кружки крупы, второй — три кружки крупы, а у третьего крупы не было. Но зато он дал охотникам 30 рублей в качестве платы за кашу. Все кашу ели поровну. Сколько рублей достанется второму охотнику, если их разделить по справедливости?
РЕШЕНИЕ: Так как 3 порции каши готовились из 5 кружек крупы, то одна порция составляет (5/3) кружки.
Первый дал две кружки крупы, значит, он имел право получить две кружки каши. Однако он взял только (5/3) кружки. 2-5/3=1/3 кружки – первый передал третьему
Второй дал три кружки крупы, значит, он имел право получить три кружки каши. Однако он взял только (5/3) кружки. 3-5/3=4/3 кружки – второй передал третьему
Видно, что второй передал третьему в 4 раза больше каши, чем первый. Значит и денег он получит в 4 раза больше. Деньги делим в отношении 1:4, то есть всего 5 частей. 30/5*4=24 рубля
ОТВЕТ: 24 рубля
Задание № 7:
Отрезок 50 см разделён на четыре неравных отрезка. Расстояние между серединами средних отрезков равно 10 см. Найдите расстояние между серединами крайних отрезков. Дайте ответ в сантиметрах.
РЕШЕНИЕ: Расстояние между серединами крайних отрезков представляет собой полусумму длин крайних отрезков и сумму длин средних отрезков.
Так как расстояние между серединами средних отрезков равно 10 см, то сумма их длин равна 2*10=20 см.
Оставшаяся длина – это сумма длин крайних отрезков: 50-20=30 см. Их полусумма тогда равна 30/2=15 см
x+2-4x+8=15-5x+3
x-4x+5x=15+3-2-8
2x=8
x=8|:2
x=4
2)-9(8-9х)=4х+5
-72+81x=4x+5
81x-4x=5+72
77x=77
x=77|:77
x=1
3)1-5х=-6х+8
-5x+6x=8-1
x=7
4)2+3х=-7х-5
3x+7x=-5-2
10x=-7
x=-7|:10
x=-0,7
5)2-3(2х+2)=5-4х
2-6x-6=5-4x
-6x+4x=5-2+6
-2x=9
x=9|:-2
x=-4,5
6)4(х-6)=5
4x-24=5
4x=5+24
4x=29
x=29|:4
x=7,25
7)х-3-4(х+1)=5(4-х)-1
x-3-4x-4=20-5x-1
x-4x+5x=20-1+3+4
2x=26
x=26|:2
x=13
8)-1-10х=-9х+1
-10x+9x=1+1
-x=2
x=2|:-1
x=-2
9)9-2(-4х+7)=7
9+8x-14=7
8x=7-9+14
8x=12
x=12|:8
x=1,5
10)9(х-6)=4х
9x-54=4x
9x-4x=54
5x=54
x=54|:5
x=10,8
11)2х+2=-3
2x=-3-2
2x=-5
x=-5|:2
x=-2,5
12)10(х+4)=9х
10x+40=9x
10x-9x=-40
x=-40
Задание № 1:
На сколько нулей оканчивается значение произведения 20^50*50^20?
2 в некой степени, очевидно, не заканчивается на 0. Значит, число нулей - 90.
ОТВЕТ: 90
Задание № 2:
Сколько существует двузначных чисел, которые после перестановки цифр увеличиваются на 75%?
РЕШЕНИЕ: Пусть было число АВ=10а+b. После перестановки получили число BA=10b+a. По условию:
Значит, если в числе цифра десятков в 2 раза больше цифры единиц, то оно попадает под наше условие.
Это числа: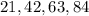
ОТВЕТ: 4 числа
Задание № 3:
Решите уравнение: |||x|−5|−5|=5. Назовите наибольший корень уравнения.
ОТВЕТ: 15
Задание № 4:
В коробке лежат чёрные, белые и красные шарики. Чёрных больше, чем 7, а белых меньше, чем 7. Вместе чёрных и красных в 2 раза больше, чем белых, а белых и красных ровно столько, сколько чёрных. Сколько всего шариков?
РЕШЕНИЕ: Пусть черных с, белых b, красных k.
Складываем уравнения:
Подставляем во второе:
Единственное возможное целое k - число 3.
Тогда k+c+b=k+3k+2k=6k=6*3=18 шариков
ОТВЕТ: 18 шариков
Задание № 5:
Стоя неподвижно на ступени эскалатора в метро Ваня поднимается наверх за одну минуту. Взбегая по ступеням неподвижного эскалатора, он добирается до верха за 40 секунд. За какое время Ваня поднимается наверх, если начинает взбегать по ступеням эскалатора, движущегося вверх? Дайте ответ в секундах.
РЕШЕНИЕ: Пусть длина расстояния L.
Если Ваня стоит неподвижно на ступени эскалатора, то скорость движения равна L/60. (Считаем в секундах, в минуте 60 секунд).
Если Ваня взбегает по ступеням неподвижного эскалатора, то скорость движения равна L/40.
Когда Ваня бежит по ступеням движущегося эскалатора, то скорости Вани и эскалатора суммируются: L/60+L/40. Тогда время определяется отношением длины к скорости:
ОТВЕТ: 24 секунды
Задание № 6:
Встретились три охотника и сварили кашу. Первый дал две кружки крупы, второй — три кружки крупы, а у третьего крупы не было. Но зато он дал охотникам 30 рублей в качестве платы за кашу. Все кашу ели поровну. Сколько рублей достанется второму охотнику, если их разделить по справедливости?
РЕШЕНИЕ: Так как 3 порции каши готовились из 5 кружек крупы, то одна порция составляет (5/3) кружки.
Первый дал две кружки крупы, значит, он имел право получить две кружки каши. Однако он взял только (5/3) кружки. 2-5/3=1/3 кружки – первый передал третьему
Второй дал три кружки крупы, значит, он имел право получить три кружки каши. Однако он взял только (5/3) кружки. 3-5/3=4/3 кружки – второй передал третьему
Видно, что второй передал третьему в 4 раза больше каши, чем первый. Значит и денег он получит в 4 раза больше. Деньги делим в отношении 1:4, то есть всего 5 частей. 30/5*4=24 рубля
ОТВЕТ: 24 рубля
Задание № 7:
Отрезок 50 см разделён на четыре неравных отрезка. Расстояние между серединами средних отрезков равно 10 см. Найдите расстояние между серединами крайних отрезков. Дайте ответ в сантиметрах.
РЕШЕНИЕ: Расстояние между серединами крайних отрезков представляет собой полусумму длин крайних отрезков и сумму длин средних отрезков.
Так как расстояние между серединами средних отрезков равно 10 см, то сумма их длин равна 2*10=20 см.
Оставшаяся длина – это сумма длин крайних отрезков: 50-20=30 см. Их полусумма тогда равна 30/2=15 см
20+15=35 см
ОТВЕТ: 35 см