Добрый день! С радостью помогу вам разобраться с задачей по нахождению частного.
Чтобы найти частное, нужно разделить одно число на другое.
1. Давайте начнем с первого примера: 10: 5/9. Чтобы разделить 10 на 5/9, мы можем использовать правило умножения на обратную величину. Обратная величина для 5/9 будет 9/5.
Таким образом, мы можем записать это как 10 * (9/5). Посчитаем: 10 * 9 = 90, а 90 / 5 = 18.
Ответ: 10: 5/9 = 18.
2. Теперь перейдем ко второму примеру: 1: 8/13. Для нахождения частного, мы будем использовать правило умножения на обратное число. Обратное число для 8/13 будет 13/8.
Запишем это как 1 * (13/8). Посчитаем: 1 * 13 = 13, а 13 / 8 = 1 5/8.
Ответ: 1: 8/13 = 1 5/8.
3. Перейдем к третьему примеру: 9/16: 36. В данном случае, мы разделим 9/16 на 36.
Когда у нас деление на число, мы можем представить это как умножение на обратную величину. Обратная величина для 36 будет 1/36.
Запишем это как (9/16) * (1/36). По правилам умножения дробей, мы умножим числители и знаменатели: 9 * 1 = 9, а 16 * 36 = 576.
Таким образом, получаем ответ: 9/16: 36 = 9/576.
4. Последний пример: 2 13/16: 4 3/8. В этой задаче, у нас деление дроби на смешанное число. Чтобы разделить одно смешанное число на другое, мы можем превратить оба числа в неправильные дроби и затем использовать правило умножения на обратное число.
Если мы переведем 2 13/16 и 4 3/8 в неправильные дроби, то получим 37/16 и 35/8 соответственно.
Теперь мы можем записать это как (37/16) * (8/35). Посмотрим на умножение числителей и знаменателей: 37 * 8 = 296, а 16 * 35 = 560.
Итак, ответ: 2 13/16: 4 3/8 = 296/560.
Вот, мы разобрали каждый из примеров и нашли их частное, объяснив каждый шаг по пути. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать.
10 :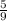 =
= 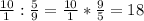
1 :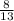 =
= 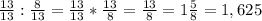
Чтобы найти частное, нужно разделить одно число на другое.
1. Давайте начнем с первого примера: 10: 5/9. Чтобы разделить 10 на 5/9, мы можем использовать правило умножения на обратную величину. Обратная величина для 5/9 будет 9/5.
Таким образом, мы можем записать это как 10 * (9/5). Посчитаем: 10 * 9 = 90, а 90 / 5 = 18.
Ответ: 10: 5/9 = 18.
2. Теперь перейдем ко второму примеру: 1: 8/13. Для нахождения частного, мы будем использовать правило умножения на обратное число. Обратное число для 8/13 будет 13/8.
Запишем это как 1 * (13/8). Посчитаем: 1 * 13 = 13, а 13 / 8 = 1 5/8.
Ответ: 1: 8/13 = 1 5/8.
3. Перейдем к третьему примеру: 9/16: 36. В данном случае, мы разделим 9/16 на 36.
Когда у нас деление на число, мы можем представить это как умножение на обратную величину. Обратная величина для 36 будет 1/36.
Запишем это как (9/16) * (1/36). По правилам умножения дробей, мы умножим числители и знаменатели: 9 * 1 = 9, а 16 * 36 = 576.
Таким образом, получаем ответ: 9/16: 36 = 9/576.
4. Последний пример: 2 13/16: 4 3/8. В этой задаче, у нас деление дроби на смешанное число. Чтобы разделить одно смешанное число на другое, мы можем превратить оба числа в неправильные дроби и затем использовать правило умножения на обратное число.
Если мы переведем 2 13/16 и 4 3/8 в неправильные дроби, то получим 37/16 и 35/8 соответственно.
Теперь мы можем записать это как (37/16) * (8/35). Посмотрим на умножение числителей и знаменателей: 37 * 8 = 296, а 16 * 35 = 560.
Итак, ответ: 2 13/16: 4 3/8 = 296/560.
Вот, мы разобрали каждый из примеров и нашли их частное, объяснив каждый шаг по пути. Если у вас возникнут еще вопросы, пожалуйста, не стесняйтесь задавать.