задачки на вероятность( После изготовления 9 одинаковых деталей проходят проверку на соответствие качеству. Вероятность брака для каждой детали одинакова и равна 0,7. Найти вероятность то, что:
1) При проверке окажется ровно 5 качественных деталей;
2) Найти наивероятнейшее количество бракованных деталей из 9 проверенных.
Пусть проводится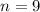 одинаковых испытаний, в каждом из которых то самое событие
одинаковых испытаний, в каждом из которых то самое событие 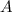 — бракованная деталь — происходит с одинаковой вероятностью
— бракованная деталь — происходит с одинаковой вероятностью 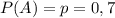 и не происходит с одинаковой вероятностью
и не происходит с одинаковой вероятностью 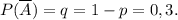 Такую совокупность условий называют схемой Бернулли с параметрами
Такую совокупность условий называют схемой Бернулли с параметрами 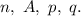
1) Если при проверке окажется ровно 5 качественных деталей, то будет 4 бракованных деталей;
Вероятность того, что в схеме Бернулли событие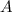 произойдет ровно
произойдет ровно 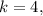 обозначают
обозначают 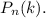
Воспользуемся теоремой Бернулли: в схеме Бернулли с параметрами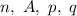 справедливо равенство
справедливо равенство 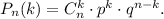 Это равенство называют формулой Бернулли.
Это равенство называют формулой Бернулли.
Имеем:
2) Частота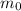 наступления события
наступления события 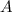 в
в 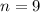 независимых повторных испытаниях называется наивероятнейшим количеством (появления этого события), если ей соответствует наибольшая вероятность. Оно определяется по формуле:
независимых повторных испытаниях называется наивероятнейшим количеством (появления этого события), если ей соответствует наибольшая вероятность. Оно определяется по формуле:
Таким образом,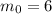 или
или 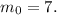
ответ: 1) 0,074; 2) 6 или 7.