Знайти: 1) точку m1, симетричну відносно прямой м1м2; 2) рівняння прямої l, що проходить через точку м1, паралельні які прямій м2м3; 3)рівняння прямої l, що проходить через точку м2, паралельно до площини p; 4)рівняння прямої l, що проходить через точку м3, перпендикулярно до площини p; 5)параметричне рівняння прямої, заданної загальними рівняннями прямих (м1; м2; м3) та (м1; м2; м4), якшо: m1(2; -4; 3); m2(5; -6; 0); m3(-1; 3; -3); m4(-3; 2; 7)
Итак, 1-я сторона равно (8+1/5) см, 2-я на (1+4/5) см меньше первой.
В первом действии найдем 2-ю сторону
1) (8+1/5) - (1+4/5) = 8+1/5-1-4/5 = (переставим слагаемые)
= 8-1-4/5+1/5=
7-4/5+1/5=
6+1-4/5+1/5=
6 +1/5+1/5=6+1/5+1/5=6+2/5=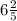
(шесть целых две пятых)
Во вторм действии найдем сумму этих сторон:
2)(8+1/5)+(6+2/5) = (раскроем скобки и сгруппируем)= 8+6+1/5+2/5 = 14+3/5 =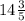
(четырнадцать целых три пятых)
В третьем действии найдем третью сторону:
3)(14+3/5) - (3+4/5) = (раскроем скобки и сгруппируем) = 14+3/5-3-4/5 = 14-3-4/5+3/5=
11-4/5+3/5=10+1-4/5+3/5=10+1/5+3/5=10+4/5 =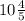
= (десять целых четыре пятых)
В четвертом действии, найдем периметр, равный сумме длин всех сторон:
4) (8+1/5)+(6+2/5)+(10+4/5) = (раскроем скобки и сгруппируем) = 8+1/5+6+2/5+10+4/5 =
= 8+6+10+1/5+2/5+4/5 = 24 + 7/5 = 24 + 1 + 2/5 = 25 + 2/5 =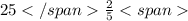
= (двадцать пять целых две пятых)
То есть положительные числа a, b, c могут быть сторонами треугольника тогда и только тогда, когда выполнены все три неравенства
a+b>c;
b+c>a;
c+a>b
У нас a=9; b=5⇒на третью сторону накладываются условия
9+5>c;
5+c>9;
c+9>5;
c>0.
Отсюда c<14; c>4.
ответ: третья сторона треугольника должна быть больше 4 см, но меньше 14 см
Рекомендация в общем виде: если даны две стороны a и b треугольника, причем a>b, то длина третьей стороны должна лежать в пределах a-b<c<a+b