Исследуем функцию на ее области определения: x є (1/e; +∞).
Слева имеем постоянную функцию, справа - монотонно возрастающую на области определения, поэтому уравнение имеет не более одного решения. Очевидно, что x = 1 - корень уравнения, а также - критическая точка функции
Вычислим знаки производной на интервалах (1/e; 1) и (1; +∞): возьмем, к примеру, числа 1/2 и e.
Имеем: , т.к. 1 - 2e < 0.
А из этого следует что числитель дроби положителен, что можно сказать и про знаменатель. Тогда f'(0,5)>0
Т.к. на интервале (1/e; 1) f'(x) > 0 , а на интервале (1; +∞) f'(x) < 0, x = 1 - точка максимума. Найдем значение максимума:\
Т.е. максимум равен f(1) = 0. Уже очевидно, что других корней уравнение иметь не будет, т.к. ни при каких других x максимум - 0 - достигаться не будет. А значит единственный корень уравнения - x = 1.
1. cos(a-b)=cos(a) * cos(b) + sin(a) *sin(b), где a и b — углы (прости, не знаю, где на клавиатуре кнопки альфа и бета, поэтому пишу просто a и b, вместо правильного обозначения. В роботе пиши именно альфа и бета, без скобок)
Исследуем функцию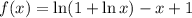
на ее области определения: x є (1/e; +∞).
Слева имеем постоянную функцию, справа - монотонно возрастающую на области определения, поэтому уравнение имеет не более одного решения. Очевидно, что x = 1 - корень уравнения, а также - критическая точка функции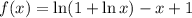
Вычислим знаки производной на интервалах (1/e; 1) и (1; +∞): возьмем, к примеру, числа 1/2 и e.
Имеем: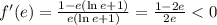
, т.к. 1 - 2e < 0.
А из этого следует что числитель дроби положителен, что можно сказать и про знаменатель. Тогда f'(0,5)>0
Т.к. на интервале (1/e; 1) f'(x) > 0 , а на интервале (1; +∞) f'(x) < 0, x = 1 - точка максимума. Найдем значение максимума:\
Т.е. максимум равен f(1) = 0. Уже очевидно, что других корней уравнение иметь не будет, т.к. ни при каких других x максимум - 0 - достигаться не будет. А значит единственный корень уравнения - x = 1.
ОТВЕТ: x = 1
Объяснение :
1. cos(a-b)=cos(a) * cos(b) + sin(a) *sin(b), где a и b — углы (прости, не знаю, где на клавиатуре кнопки альфа и бета, поэтому пишу просто a и b, вместо правильного обозначения. В роботе пиши именно альфа и бета, без скобок)
cos32° *cos cos15° +sin 32° *sin 15°= cos(32-15)°= cos17°
2. Немного не понял запись самого выражения. Если я правильно угадал, то вот решение:
(cosx) ^2- (sinx) ^2= cos2x
sin2x * 26/cos 2x= sin2x/cos 2x *26= tg2x*26= 26tg2x
3. Во вложении
4. Некоректное задание cosa≠35