Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов:
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
Из равенства заметим, что второй множитель можно разложить на множители по формуле суммы кубов
В 1 слитке 5*30/100 = 1,5 кг меди. Во 2 слитке 3*30/100 = 0,9 кг меди. В 3 слитке x кг меди, а его вес y кг. Если 1 слиток сплавить с 3, получится (1,5+x) кг меди при массе (5+y) кг. (5 + y)*0,56 = 1,5 + x Если 2 слиток сплавить с 3, получится (0,9+x) кг меди при массе (3+y) кг. (3 + y)*0,6 = 0,9 + x Составляем систему { 56*5 + 56y = 150 + 100x { 60*3 + 60y = 90 + 100x Вычитаем из 1 уравнения 2 уравнение 280 + 56y - 180 - 60y = 150 - 90 100 - 4y = 60 y = 10 280 + 56*10 = 150 + 100x 280 + 560 - 150 = 100x x = 6,9 В 3 слитке 6,9 кг меди при массе слитка 10 кг. В слитке из всех трех кусков будет 1,5+0,9+6,9 = 9,3 кг меди при массе 5+3+10 = 18 кг. Процентное содержание 9,3/18 = 0,517 = 51,7%
Условие. сумма второго и восьмого членов бесконечно убывающей геометрической прогрессии равна.325/128, а сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой же прогрессии. Найти первый член прогрессии и знаменатель.
Сумма второго и восьмого членов: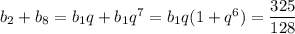
Сумма второго и шестого членов, уменьшенная на 65/32, равна четвертому члену этой прогрессии:
Из равенства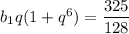 заметим, что второй множитель можно разложить на множители по формуле суммы кубов
заметим, что второй множитель можно разложить на множители по формуле суммы кубов
Подставляем данные, получим
ответ: 5; 0.5 и -5; -0.5.
В 3 слитке x кг меди, а его вес y кг.
Если 1 слиток сплавить с 3, получится (1,5+x) кг меди при массе (5+y) кг.
(5 + y)*0,56 = 1,5 + x
Если 2 слиток сплавить с 3, получится (0,9+x) кг меди при массе (3+y) кг.
(3 + y)*0,6 = 0,9 + x
Составляем систему
{ 56*5 + 56y = 150 + 100x
{ 60*3 + 60y = 90 + 100x
Вычитаем из 1 уравнения 2 уравнение
280 + 56y - 180 - 60y = 150 - 90
100 - 4y = 60
y = 10
280 + 56*10 = 150 + 100x
280 + 560 - 150 = 100x
x = 6,9
В 3 слитке 6,9 кг меди при массе слитка 10 кг.
В слитке из всех трех кусков будет 1,5+0,9+6,9 = 9,3 кг меди при
массе 5+3+10 = 18 кг.
Процентное содержание 9,3/18 = 0,517 = 51,7%