Розв’язування задач за до систем лінійних рівнянь:
Майстер і учень повинні були виготовити 69 деталей. Після того, як учень працював 3 години, до роботи приєднався майстер, і вони разом закінчили завдання за 2 години. Скільки деталей за годину виготовляє майстер і скільки – учень, якщо майстер за 3 години виготовляє стільки ж деталей, скільки учень за 4 години?

Задание 1.

ответ: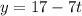  

  или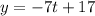  

Задание 2. Две семьи отправились на детский утренник. Первая семья купила два детских билета и один взрослый и всего заплатила 390 рублей. Вторая семья купила три детских билета и два взрослых и всего заплатила 685 рублей. Сколько стоит один детский билет и сколько стоит один взрослый билет?

Решение.

Пусть х руб. - стоит один детский билет.

По условию 2 детских билета и один взрослый стоят 390 рублей, значит,

(390-2х) руб. - стоит один взрослый билет.

Ещё в условии сказано, что 3 детских билета и 2 взрослых стоят всего 685 рублей.

Получаем уравнение:

3х + 2 · (390-2х) = 685

3х + 780 - 4х = 685

-х = - 95

х = - 95 : (-1)

х = 95 руб. - стоит один детский билет.

390-2·95=200 руб. - стоит один взрослый билет.

Детский билет стоит  95 рублей,

а взрослый билет стоит  200 рублей.

В решении.

Объяснение:

На рисунке два графика: парабола - уравнение у = -х² и прямая, уравнение у = -25.

Почему парабола у = -х²? Потому, что ветви направлены вниз (знак минус перед х²), вершина в начале координат (нет смещения ни по оси Ох, ни по оси Оу), и при значении х=±5  у= -25, х в квадрате.

Приравнять правые части (левые равны):

-х² = - 25

х² = 25

х₁,₂ = ±√25

х₁ = -5

х₂ = 5.

Корни квадратного уравнения являются абсциссами (значениями х) точек пересечения графиков. Ордината (значение у) = -25.

Координаты точек пересечения (-5; -25);  (5; -25).

Квадратное уравнение -х² = - 25 можно записать в виде:

-х² + 25 = 0.