теперь нужно обозначить данные две точки на оси ОХ. Так как а=2. то ветви параболы направлены вверх, следовательно решением данного неравенства будет промежуток: х∈(-∝;-1,5)∪(2;+∝) Вопрос в задаче некорректный, так как наибольшего не существует, то возможно они хотели спросить о наименьшем положительном, то ответ будет:3
(a1+d)(a1+4d)=160(2) если подставить (1) в(2) то получим (8-d+d) (8-d+4d)=160⇒8(8+3d)=160⇒8+3d=20⇒3d=20-8=12⇒d=4 и теперь подставим найденное значение в (1) то получим a1=8-4=4. Для нахождения суммы воспользуемся формулой:
Обозначим а-длина, в-ширина прямоугольника и с - диагональ. Р=2(а+в)=70⇒а+в=35⇒а=35-в. По теореме Пифагора:a^2+в^2=c^2
(35-в)^2+в^2=25^2⇒1225-70в+2в^2=625⇒2в^2-70в+600=0⇒в^2-35в+300=0⇒(в-15)(в-20)⇒в1=15 и в2=20. так как в ширина то в=15 и а=20 и следует что S=а*в=20*15=300 cм^2
Объяснение: 17. Сначала нужно решить уравнение: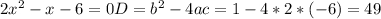
18.а1+а3=16⇒а1+а1+2d=16⇒2a1+2d=16⇒a1+d=8⇒a1=8-d(1)
(a1+d)(a1+4d)=160(2) если подставить (1) в(2) то получим (8-d+d) (8-d+4d)=160⇒8(8+3d)=160⇒8+3d=20⇒3d=20-8=12⇒d=4 и теперь подставим найденное значение в (1) то получим a1=8-4=4. Для нахождения суммы воспользуемся формулой: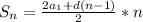
Обозначим а-длина, в-ширина прямоугольника и с - диагональ. Р=2(а+в)=70⇒а+в=35⇒а=35-в. По теореме Пифагора:a^2+в^2=c^2
(35-в)^2+в^2=25^2⇒1225-70в+2в^2=625⇒2в^2-70в+600=0⇒в^2-35в+300=0⇒(в-15)(в-20)⇒в1=15 и в2=20. так как в ширина то в=15 и а=20 и следует что S=а*в=20*15=300 cм^2
a) (-1; 4), (1; 0)
б) [-∞; -1) ∪ (1; +∞)
Объяснение:
a) Точки экстремума определяются при приравнивании производной к нулю:
y' = 3x^2 - 3 = 0
3x^2 = 3
x^2=1
x1 = -1
x2 = 1
Находим y точек по заданному x:
y1 = (-1)^3 - 3 * (-1) + 2 = 4
y2 = (1)^3 - 3 * (1) + 2 = 0
Получаются точки: (-1; 4), (1; 0)
б) Промежутки возрастания можно определить расставив знаки между промежутками экстемумов:
x1x2>
+ - +
y'(-2) = 9, значит слева от x1 плюс (функция возрастает)
y'(0) = -3, значит между x1 и x2 минус (функция убывает)
y'(2) = 9, значит справа от x2 плюс (функция возрастает)
Промежутки возростания: [-∞; -1) ∪ (1; +∞)