Если тригонометрические соотношения в прямоугольном треугольнике ещё не изучены, можно воспользоваться этим
1. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, тогда длина гипотенузы с = 2R = 2•3 = 6(см).
2. По условию один из острых углов треугольника равен 60°, тогда второй острый угол равен 90° - 60° = 30°. Напротив него лежит катет, равный половине гипотенузы, а = 6:2= 3 (см).
3. По теореме длина второго катета b = √(36 - 9) = √27 = 3√3(см).
Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3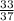
,AD=37-3
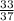=33
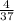
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD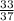=3
*33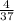
=
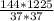, CD=√(
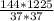)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10
3√3/2 см.
Объяснение:
Если тригонометрические соотношения в прямоугольном треугольнике ещё не изучены, можно воспользоваться этим
1. Центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы, тогда длина гипотенузы с = 2R = 2•3 = 6(см).
2. По условию один из острых углов треугольника равен 60°, тогда второй острый угол равен 90° - 60° = 30°. Напротив него лежит катет, равный половине гипотенузы, а = 6:2= 3 (см).
3. По теореме длина второго катета b = √(36 - 9) = √27 = 3√3(см).
4. S = 1/2ab,
S = 1/2• c • h, тогда
1/2•a•b = 1/2• c • h,
ab = ch,
h = (ab)/c = (3•3√3)/6 = 3√3/2 (см).