Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости, т.е. не параллельны и не пересекаются.
Признак скрещивающихся прямых: Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Дано: a⊂α, b∩α = M, M∉a.
Доказать: прямые а и b скрещивающиеся.
Доказательство:
Предположим, что прямые а и b не являются скрещивающимися, тогда через них можно провести плоскость. В этой плоскости окажется и точка М. Но через прямую а и точку М можно провести единственную плоскость. Значит, плоскость, проходящая через прямые а и b совпадает с плоскостью α. Но тогда прямая b лежит в плоскости α. Это противоречит условию: прямая b пересекает плоскость α. Предположение неверно, прямые а и b скрещивающиеся.
По признаку параллелограмма (если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам - то он параллелограмм), делаем вывод, что ABCD - параллеллограмм
По формуле расстояний между двумя точками, задаными координатами
находим длины диагоналей AC и BD
Диагонали равны
По признаку прямоугольника (если диагонали параллелограмма равны - то он парямоугольник), делаем вывод, что ABCD - прямоугольник.
Две прямые называются скрещивающимися, если они не лежат в одной плоскости, т.е. не параллельны и не пересекаются.
Признак скрещивающихся прямых:
Если одна прямая лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
Дано: a⊂α, b∩α = M, M∉a.
Доказать: прямые а и b скрещивающиеся.
Доказательство:
Предположим, что прямые а и b не являются скрещивающимися, тогда через них можно провести плоскость. В этой плоскости окажется и точка М. Но через прямую а и точку М можно провести единственную плоскость. Значит, плоскость, проходящая через прямые а и b совпадает с плоскостью α. Но тогда прямая b лежит в плоскости α. Это противоречит условию: прямая b пересекает плоскость α.
Предположение неверно, прямые а и b скрещивающиеся.
По формуле середины отрезка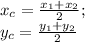
ищем координаты середины отрезков AC и BD
АС: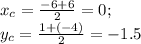
(0;-1.5)
BD: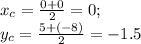
(0;-1.5)
Середины совпадают
По признаку параллелограмма (если диагонали четырехугольника пересекаются и в точке пересечения делятся пополам - то он параллелограмм), делаем вывод, что ABCD - параллеллограмм
По формуле расстояний между двумя точками, задаными координатами
находим длины диагоналей AC и BD
Диагонали равны
По признаку прямоугольника (если диагонали параллелограмма равны - то он парямоугольник), делаем вывод, что ABCD - прямоугольник.
Доказано