Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора:
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).
Один из сторон — перпендкулярен прямой, тоесть эта же сторона образует 2 прямых угла, тоесть, треугольник — прямоугольный.
Наклонная(или гипотенуза) — равна 12 сантиметров, и с прямой она образует угол 30-и градусов.
Теорема о 30-градусном угле прямоугольного треугольника такова: катет, противолежащий углу 30-градусов в прямоугольном треугольнике — равен половине гипотенузы
А перпендикуляр лежит на против этого же угла 30-градусов, тоесть — прерпендикуляр равен половине наклонной, тоесть перпендикуляр равен: 12/2 = 6.
Теперь мы знаем гипотенузу, и один и катетов, чтобы найти проекцию(второй катет) — используем теорему Пифагора: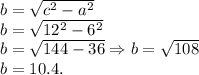
Вывод: перпендикуляр равен — 6 см; проекция равна — 10.4см(или √108, как удобнее).
Решение:
ВD- высота, медиана и биссектрисса равнобедренного треугольника ∆АВС;
АD=DC;
DC=AC/2=16/2=8ед.
∆ВDC- прямоугольный треугольник
Теорема Пифагора
ВD=√(BC²-DC²)=√(17²-8²)=
=√((17+8)(17-8))=√(25*9)=5*3=15ед.
ответ: х=15ед.
№6)
RN=NM=6ед ∆RNM-равносторонний;
RK- высота, медиана и биссектрисса.
NK=KM
NK=NM/2=6/2=3
∆RKN- прямоугольный треугольник
По теореме Пифагора
RK=√(RN²-NK²)=√(6²-3²)=
=√((6-3)(6+3))=√(3*9)=3√3ед.
ответ: х=3√3ед.
№7)
РТ=PR/2=x/2.
По теореме Пифагора
RP²-PT²=RT²
Составляем уравнение.
х²-(х/2)²=8²
х²-х²/4=64. |×4.
4х²-х²=256
3х²=256. |÷3
х²=256/3
х=√(256/3)
х=16/√3
х=16√3/3 ед
ответ: х=16√3/3 ед