Реши задачу УМОЛЯЯЯЮЮЮ

Дано: КА - перпендикуляр к плоскости ABC, KB перпендикулярен BC, AC=13,BC=5 угол альфа = 45

Доказать: треуголтник АВС - прямоугольный, (KAC)перпендикулярна (ABC)

Найти: KA

Доказательство: 

а) КА - перпендикуляр к плоскости ABC

    КВ - наклонная

    АВ - проекция наклонной на плоскость

по теореме обратной ТТП АВ перпендикулярна СВ,тогда

угол АВС = 90 градусов, следовательно треугольник АВС - прямоугольный.

б) КАВ линейный угол двугранного угла ВКАС. т.к. КА - перпендикуляр к плоскости АВС угол КАВ = 90 градусов, следовательно, пересекающиеся плоскости КАС и АВС перпендикулярны

в)1. по т. пифагора АВ=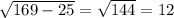  

2. угол КАВ= 90, угол КВА=45, тогда угол АКВ=180-(90+45)=45

угол КВА=углу АКВ, следовательно треугольник АВК - равнобедренный, с равными сторонамми КА и ВА, тогда

КА=ВА=12 (см)

Решение: Боковые стороны равнобедренного треугольника равны:

AC=BC

По теореме Пифагора

AC=корень(CD^2+(AB\2)^2)

AC=корень(5^2+(12\2)^2)=корень(61) см

ВС=корень(61) см

Полуперитр треугольника АВС равен поллусумме сторон треугольника р=(АВ+ВС+АС)\2

р=(12+корень(61)+корень(61))\2=корень(61)+6 cм

Площадь треугольника равна половине произведения высоты на длину основания

S (ABC) =1\2*CD*AB

S=1\2*12*5=30 см^2

Радиус треугольника равен отношению площади треугольника к его полупериметру

r (ABC)= S\p

r=30\(корень(61)+6)=30\(61-36)*(корень(61)-6)=

=6\5*(корень(61)-6) cм.

ответ:6\5*(корень(61)-6) cм.