Решите 8,9,10. по действиям, напишите, что да как делали.

Два возможных случая:

1)

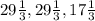
2)

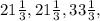
Объяснение:

Т.к. треугольник равнобедренный, то по определению имеет 2 равные боковые стороны.

Случай 1. Пусть основание меньше боковой стороны, тогда основание = x, а боковые стороны x + 12. Периметр - это сумма всех сторон, так что составим уравнение:

x + (x+12) + (x+12) = 76

3x + 24 = 76

3x = 76 -24

3x = 52

x = 52: 3 =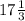  - основание, значит боковая сторона = x + 12 =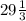

Случай 2. Пусть основание больше боковой стороны, тогда основание = x, а боковые стороны x - 12.

Составляем уравнение

x + (x-12) + (x-12) = 76

3x - 24 = 76

3x = 76 + 24

3x = 100

x = 100:3 =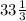 , ⇒ боковая сторона = x - 12 =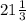

1) Примем угол при вершине за х, тогда угол при основании 4х
   Сумма внутренних углов треугольника равна 180°,
   тогда: х + 4х + 4х = 180
                          9х = 180
                           х = 20    4х = 80

ответ: угол при вершине 20°, углы при основании 80°

2) Примем угол при основании за х, тогда угол при вершине 4х.
   Следовательно, 2х + 4х = 180
                                   6х = 180
                                     х = 30          4х = 120

ответ: Угол при вершине 120°, углы при основании 30°