УМОЛЯЮ Все рёбра тетраэдра ABCD равны. Через сторону АВ проведена плоскость, перпендикулярная ребру CD. Найдите величину двугранного угла, образованного этой плоскостью с плоскостью грани ABC.

Показать ответ

Ответ:

nikky228like

21.12.2021 19:31

$\alpha=arccos\dfrac{\sqrt{6}}{3}$

Объяснение:

Пусть К -середина CD.

Тетраэдр правильный, все грани - правильные треугольники, тогда АК⊥CD как медиана и высота ΔACD, ВК⊥CD как медиана и высота ΔBCD, значит плоскость (АВК)⊥CD.

АК = КВ (медианы равных равносторонних треугольников)

Пусть Н - середина АВ.

СН⊥АВ как медиана и высота ΔАВС, КН⊥АВ как медиана и высота равнобедренного треугольника АКВ, значит

∠КНС - линейный угол двугранного угла между плоскостями (АКВ) и (АВС) - искомый.

∠KCH = α.

Пусть а - ребро тетраэдра.

$CH=AK=\dfrac{a\sqrt{3}}{2}$ - высоты равных равносторонних треугольников,

$CK=\dfrac{a}{2}$

Из прямоугольного треугольника АКН по теореме Пифагора:

$KH=\sqrt{AK^2-AH^2}=\sqrt{\dfrac{a^2\cdot 3}{4}-\dfrac{a^2}{4}}=$

$=\sqrt{\dfrac{2a^2}{4}}=\dfrac{a\sqrt{2}}{2}$

Из ΔКНС по теореме косинусов:

$\cos\alpha =\dfrac{KH^2+CH^2-CK^2}{2\cdot KH\cdot CH}$

$\cos\alpha =\dfrac{\dfrac{2a^2}{4}+\dfrac{3a^2}{4}-\dfrac{a^2}{4}}{2\cdot \dfrac{a\sqrt{2}}{2}\cdot \dfrac{a\sqrt{3}}{2}}$

$\cos\alpha =\dfrac{a^2}{\dfrac{a^2\sqrt{6}}{2}}=\dfrac{2}{\sqrt{6}}=\dfrac{\sqrt{6}}{3}$

$\alpha=arccos\dfrac{\sqrt{6}}{3}$

УМОЛЯЮ Все рёбра тетраэдра ABCD равны. Через сторону АВ проведена плоскость, перпендикулярная ребру

0,0(0 оценок)

Ответ:

npletnikova

21.12.2021 19:31

$\angle(ABC,ABK) = \arcsin \left ( \dfrac{\sqrt{3} }{3} \right )$

Объяснение:

Дано: ABCD - тетраэдр, AC = BC = AB = DA = DB = DC, ABK ⊥ CD

Найти: ∠(ABC, ABK) - ?

Решение: Пусть BD = x. Так как по условию AC = BC = AB = DA =

= DB = DC, то x = AC = BC = AB = DA = DB = DC. Проведем из точки K перпендикуляр к прямой AB в точку F. Так как точки A,B ∈ ABC и A,B ∈ ABK, то ABC ∩ ABK = AB.

Так как (F ∈ AB, ABC ∩ ABK= AB ⇒ AB ⊂ ABK) ⇒ F ∈ ABK, то KF ⊂ ABK.

Так как по условию ABK ⊥ CD, то по определению перпендикулярности прямой плоскости, прямая перпендикулярная плоскости, перпендикулярна любой прямой лежащей в этой плоскости, тогда KF ⊥ CD, так как KF ⊂ ABK. Так как KF ⊥ CD и KF ⊥ AB по построению, то по теореме о трех перпендикулярах CF ⊥ AB.

Так как CF ⊥ AB и KF ⊥ AB, то угол ∠KFC является линейным углом двухгранного угла ∠(ABC, ABK), то есть ∠(ABC, ABK) = ∠KFC.

Так как по условию AC = BC = AB = DA = DB = DC, то тетраэдр ABCD - правильный по определению. По свойствам правильного тетраэдра все его грани правильные треугольники, тогда треугольник ΔABC - правильный. По свойствам правильного треугольника все его углы равны 60°, тогда ∠CAB = 60°. Рассмотрим треугольник ΔCAF. Так как CF ⊥ AB, то треугольник ΔCAF - прямоугольный.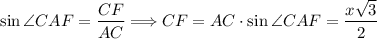 $\sin \angle CAF = \dfrac{CF}{AC} \Longrightarrow CF = AC \cdot \sin \angle CAF = \dfrac{x\sqrt{3} }{2}$ . Так как CF ⊥ AB, то CF - высота правильного треугольника ΔABC. По свойствам правильного треугольника все его высоты являются медианами и биссектрисами, тогда точка F - середина отрезка AB. Так как все грани правильного тетраэдра правильные треугольники, то треугольник ΔADB - правильный. Проведем отрезок DF в треугольнике ΔΔADB. Так как точка F - середина отрезка AB, то отрезок DF - медиана, а по свойствам правильного треугольника биссектриса и высота. Так как по свойствам правильного тетраэдра(ABCD) все его грани равны между собой треугольник, то соответствующие элементы треугольников равны, тогда CF = DF как высоты правильных треугольников, следовательно треугольник ΔCFD - равнобедренный с основанием CD. Так как FK ⊥ CD, то по теореме высота равнобедренного треугольника проведенная к основанию(CD) является медианой и биссектрисой, то есть

CK = KD = CD : 2 = x : 2 = 0,5x.

Рассмотрим прямоугольный треугольник ΔCKF.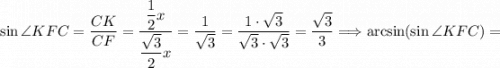 $\sin \angle KFC = \dfrac{CK}{CF} = \dfrac{\dfrac{1}{2}x }{\dfrac{\sqrt{3} }{2}x } = \dfrac{1}{\sqrt{3} } = \dfrac{1 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3} } = \dfrac{\sqrt{3}}{3} \Longrightarrow \arcsin ( \sin \angle KFC)=$

$= \arcsin \left ( \dfrac{\sqrt{3} }{3} \right );$

0,0(0 оценок)

Ответ:

SlowMoe

27.01.2024 11:56

Привет! Рад, что ты обратился ко мне за помощью. Давай разберемся вместе в этой задаче.

В задании говорится, что у нас есть тетраэдр ABCD, у которого все ребра равны. Так как тетраэдр имеет 4 грани, то нам нужно найти величину двугранного угла, образованного плоскостью, проведенной через сторону AB, с плоскостью грани ABC.

Для начала, представим себе тетраэдр ABCD в пространстве:

A
/|\
/ | \
/ | \
B---C---D

Плоскость, проведенная через сторону AB, будет пересекать тетраэдр по некоторому отрезку. Нам нужно найти величину угла, образованного этим отрезком и плоскостью грани ABC.

Посмотрим на грань ABC:

A
/ \
/ \
/_____\ B
C

Грань ABC представляет собой плоскость, а отрезок, проведенный через сторону AB, будет как раз линией пересечения этой грани с нашей плоскостью. Итак, нам нужно найти угол между этой линией и плоскостью грани ABC.

Для того чтобы найти этот угол, мы можем использовать информацию о свойствах параллельных прямых. Если две прямые параллельны, то угол между ними равен 0 градусов.

Вернемся к нашему отрезку, проведенному через сторону AB, и плоскости грани ABC. Поскольку плоскость, перпендикулярная ребру CD, проходит через сторону AB, то эта плоскость параллельна плоскости грани ABC.

Это означает, что угол между этими двумя плоскостями равен 0 градусов.

Таким образом, величина двугранного угла, образованного плоскостью, проведенной через сторону AB, с плоскостью грани ABC, равна 0 градусов.

Надеюсь, что я смог помочь тебе разобраться в этой задаче. Если у тебя возникнут еще вопросы, не стесняйся обращаться!

0,0(0 оценок)

Популярные вопросы: Геометрия