В основі піраміди лежить прямокутний трикутник з гіпотенузою 12 см. Знайдіть висоту піраміди, якщо всі бічні ребра нахилені до площини основи під кутом 30°.
Оскільки всі бічні ребра нахилені до площини основи під кутом 30°, то висота проектується в центр кола, описаного навколо трикутника АСВ, а оскільки Δ АВС - прямокутний, то т. О - середина гіпотенузи (АО=ОВ)
2√3 см
Объяснение:
∠ С = 90°, АВ - гіпотенуза
Оскільки всі бічні ребра нахилені до площини основи під кутом 30°, то висота проектується в центр кола, описаного навколо трикутника АСВ, а оскільки Δ АВС - прямокутний, то т. О - середина гіпотенузи (АО=ОВ)
АО = 12/2= 6см
Δ АОS - прямок., tg∠SAO =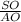
SO = 6*tg30° = 6*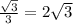 cм
cм